Ciaglosc funkcji Definicja: Prosze o pomoc i dokladne wytlumaczenie (tzn w sumie gotowca Zbadaj ciaglosc funkcji f w punkcie x₀ jezeli

	x2−4
f(x)=		dla x∊R\{−1,1}
	1−x2

1 dla x∊{−1,1} x₀=1

PW: Podziel licznik i mianownik przez x² i licz granice jednostronne w x₀.

Definicja: Jest PW pewien problem nie zwiazany z tym ze nie umiem tego podzielic Ale tutaj bedzie lim x→1⁻ i lim x→1⁺ i nie wiem z ktorych funkcji liczyc Poza tym beda koncowki ktore nie wiadomo do czego zbiegaja no ale napiszse

	x2(1−4/x2)
lim x→1−		tylko tyle moge na teraz napisac
	x2(1/x2−1)

Definicja: MIalem tez problem z tym czy w ogole x₀1 nalezy do dziedziny ale tak bo f(x)=1 dla x=1 wiec tak

PW: Co za "końcówki, które nie wiadomo do czego zbiegają"?

Eta: "końcówka" ?

Definicja:

	4
Na trapezie bylo mowione ze jesli x→∞ to np		→0
	x2

	4		1
jesli x→1 to np jak tutaj		czy		nie wiadomo do czego daza wiec
	x2		x2

dlatego nie mozna bylo wylaczac x² przed nawias Jednak wykonalem Twoje polecenie Z funkcjami typu x≤0 i x>0 dla x₀ = coś tam nie mam problemu z wyznaczeniem wartosci funkcji i granic Bo liczylem granice jednostronne z jednej i grugiej funkcji Przyklad takiej funkcji f(x)= (−(x+0,5)² dla x<−0,5 ( 2x+1 dla x≥−0,5 i x₀= −0,5

PW:

	4
Jeżeli x→1, to		nie wiadomo do czego dąży?
	x2

Definicja: Dlatego prosilem w sumie o gotowca jak postepowac z takimi funkcjami sklejanymi W sumie nie wiem tez dlaczego mam liczyc granice z tej wymiernej?

Definicja: Bo tak Funkcja jest okreslona w punkcie x₀=1 i f(1)=1 I teraz te nieszczesne granice

PW: Pogubiłeś się zupełnie z tymi wątpliwościami. Nie umiem Ci pomóc.

Definicja: NIc nie szkodzi . Dziekuje za juz .

jc: Definicja, czy wydaje Ci się, że zapisanie w tak dziwny sposób licznika i mianownika w czymś pomoże? 18:02. Ten zwyczaj prześladuje studentów przez pierwsze lata i zwykle prowadzi do złego (złej oceny).

Definicja: To jak go mam zapisac ? Nie mam tutaj piora zeby te x² skrocic

	1−4/x2
Moglem ewentualnie zapisac dalel = lim x→1−
	1/x2−1

Dalej to i tak mi niczym nie pomaga . Przedsatwilem swoje watpliwosci i jesli potrafisz pomoc bede wdzieczny

Definicja: Przede wszystkim Dlaczego mam liczyc granice z funkcji wymiernej ? bo ? Potem dopiero kwestia liczenia granic

tip : piszesz: > W sumie nie wiem tez dlaczego mam liczyc granice z tej wymiernej? a jaka jest definicja ciągłości w punkcie? w skrócie granica (obustronna) w punkcie musi być równa wartości funkcji w tym punkcie. wartość w punkcie masz − jest równa 1. teraz musisz policzyć granicę w x₀=1. jeżeli ta granica (obustronna) będzie równa 1, to funkcja jest ciągła w tym punkcie. jeżeli granica (obustronna) nie będzie równa 1 to funkcja jest nieciągła w tym punkcie. pytasz "dlaczego mam liczyc granice z tej wymiernej?" − nie wiem skąd wątpliwości. czy dlatego, że wymierna nie jest określona w 1? jeśli stąd wątpliwości to niepotrzebnie, bo przecież granicę można sobie liczyć w punkcie, który do dziedziny nie należy. jeśli jest inny powód wątpliwości to postaraj się go opisać. polecam obejrzeć sobie wykład: https://www.youtube.com/watch?v=Uq-lcI6mDOU

Definicja: Z definicji ciaglosci funkcji w punkcie wynika to ze nie ma sensu zastananwiac sie nad ciagloscia funkcji w punkcie ktory nie nalezy do jej dziedziny I wlasnie moja watpliwosc wynika z tego co napisales /as ze wymierna nie jest okreslona w punkcie x₀=1

tip : sama wymierna nie musi być określona w punkcie x₀=1. ważne żeby w ogóle ten punkt do dziedziny funkcji należał i tak też jest w tym zadaniu, bo dla x=1 wartość jest równa 1. bo generalnie mówiąc Ty nie sprawdzasz ciągłości tej funkcji wymiernej samej w sobie, a ciągłość tej całej funkcji zapisanej klamrą. zapisana klamrą funkcja jest określona w jedynce, więc jest sens żeby zastanawiać się nad ciągłością w tym punkcie.

Definicja: Dobrze . I tak bede musial wrocic do klasy 2 z materialem . Teraz jesli mozesz to rozpisz mi te granice . dzieki

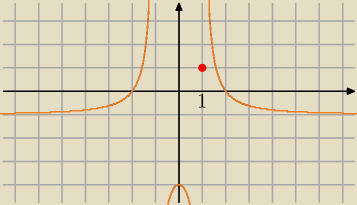
tip : tak podglądowo rysunek − może pomoże zrozumieć dlaczego liczenie granicy funkcji wymiernej w x₀=1 będzie konieczne. [ogólnie do zrobienia tego zadania rysunek nie jest potrzebny − ale jak mówię, może pomóc w zrozumieniu]

Definicja: Ponawiam prosbe w policzeniu tych granic

iteRacj@:

x2−4
1−x2

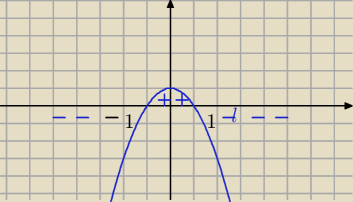
rysunek ilustruje wartości mianownika

	x2−4		1−4		−3
limx→−1−		=[		]=[		]=∞
	1−x2		0−		0−

	x2−4		−3
limx→−1+		=[		]= −∞
	1−x2		0+

	x2−4		−3
limx→1−		=[		]= −∞
	1−x2		0+

	x2−4		−3
limx→1+		=[		]= ∞
	1−x2		0−

iteRacj@: funkcja nie jest ciągła dla argumentów x=−1 i x=1

iteRacj@: *funkcja f(x) podana 17:44

Definicja: Dziekuje Ci iteRacj@ za dokladne rozpisanie Ale i tak musze wrocic do klasy 2

iteRacj@: a czy jest dla Ciebie jasne, czemu f(x) nie jest ciągła?

Definicja: Tak iteRacj@ Granice w 1 nie sa rowne to jedno a po drugie musialyby byc rowne wartosci fucji w x₀=1

iteRacj@: a dlaczego masz wracać akurat do 2 klasy? teraz granice i ciągłość są w 3−ciej

Definicja: Bo mialem granice niewlasciwe i w nieskonczonosci w klasie 2

iteRacj@: rzeczywiście, to zależy od podręcznika niektórzy mają to już w 2 klasie