log Maikkkk: Wykres funkcji f(x)=log(o podstawie 2) z (x²−10x+25): A) nie ma osi symetrii B) ma oś symetrii o równaniu x = −5 C) ma oś symetrii o równaniu y = 5 D) ma oś symetrii o równaniu x = 5 Jak to rozwiązać?

PW: x²−10x+25=(x−5)² log₂((x−5)²) nie jest zdefiniowany dla liczby x₀=5, natomiast dla leżących symetrycznie względem x₀ liczb x₀−u i x₀+u osiąga te same wartości, bo (5−u−5)²=(5+u−2)². Oznacza to, że prosta o równaniu x=5 jest osią symetrii wykresu.

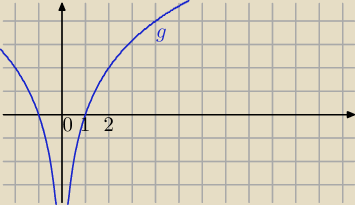
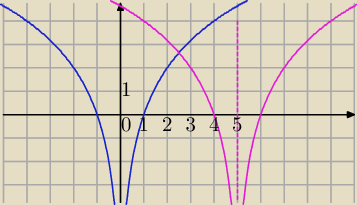
Mila: 1) g(x)=x² ma wykres jak na rysunku 2) f(x)=log₂(x²−10x+25)=log₂(x−5)² wykres tej funkcji powstanie przez przesuniecie o 5 jednostek w prawo wykresu funkcji g(x) D: x−5≠0 x=5 − oś symetrii wykresu tej funkcji niestety rysunek nie wchodzi, może później.

Mila:

Mila: