trapez mat-fiz: W trapezie ABCD o podstawach |AB|=a i |DC|=b gdzie a>b>0 poprowadzono odcinek KL równoległy do podstaw, który podzielił trapez na dwa trapezy o równych polach. Wykaż,że |KL|>√ab

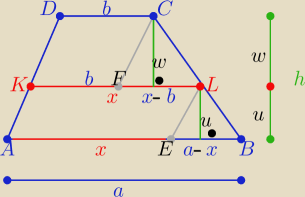
Eta: 1/ przejrzysty rysunek zgodnie z treścią zadania

	a+x		x+b
2/ a>b>0 i P1=P(ABLK)=		*u i P2=P(KLDC)=		*w
	2		2

z treści zadania P₁=P₂

	w		a+x
to		=
	u		b+x

3/ z podobieństwa trójkątów EBL i FLC z cechy (kkk)

	w		x−b
		=
	u		a−x

	a+x		x−b
zatem:		=		⇒ a2−x2= x2−b2 ⇒ 2x2=a2+b2
	b+x		a−x

	a2+b2
to x=|KL|=√		−−− średnia kwadratowa długości podstaw
	2

=================

	a2+b2
teraz tylko należy wykazać ,że √		>√ab
	2

to nierówność między średnią kwadratową i średnią geometryczną podstaw a>b>0

	a2+b2
(a−b)2>0 ⇔ a2+b2>2ab ⇔		>ab /√
	2

	a2+b2
√		>√ab
	2

zatem |KL|>√ab ========== c.n.w