asymptoty Gość: zbadaj asaymptoty funkcji f(x) = √2x−x²/x

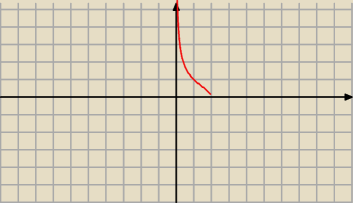
Adam: x∊(0, 2] lim_x→0⁺ f(x) = ∞ mamy jedną asymptotę z prawej x=0

Gość: ale czy dziedzina nie bedzie obustronnie domknieta ? pod pierwiastkiem jest funkcja kwadratowa a z liczenia delty wychodzą 2 miejsca zerowe

Basia: 2x−x²≥0 ∧ x≠0 x(2−x)≥0 ⇔ x∊<0;2> mamy więc D=(0;2>

	0
dla x=2 mamy f(2) =		=0 i żadnej asymptoty tam być nie może
	2

	f(x)
asymptot ukośnych też nie będzie bo nie da się policzyć limx→±∞		skoro dziedziną
	x

jest przedział (0,2> możemy więc mieć jedynie jakąś asymptotę dla x→0⁺ czyli trzeba policzyć

	√2x−x2		2−2x		2
limx→0+		= (H) limx→0+		= [		]= +∞
	x		2√2x−x2		0+

mamy asymptotę pionową prawostronną x=0