Woda: Sześcian przecięto płaszczyzną zawierającą przekątną podstawy i przecinającą ścianę boczną w 2/3 jej wysokości. Kąt α jest kątem, jaki tworzy płaszczyzna przekroju z podstawą sześcianu. Oblicz cosinus kąta przyległego do kąta α

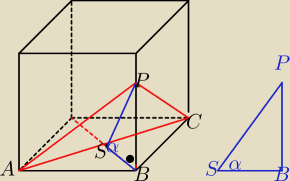
Basia: trójkąt APC jest równoramienny spodek wysokości jest środkiem podstawy AC α to kąt BSP; kat PBS jest prosty

	SB
cosα=
	SP

	2a
BP =
	3

	a√2
SB=
	2

	4a2		2a2		16a2+18a2		34a2
SP2 = BS2+BP2 =		+		=		=
	9		4		36		36

	a√34
SP =
	6

a√2

a√34

a√2

6

3√2

3√68

cosα=

/

=

*

=

=

=

2

6

2

a√34

34

34

3*2√17		3√17
	=
34		17

cos(180−α)=cosα sprawdź obliczenia, mogłam się pomylić

Eta: Hej Basia wszystko gra tylko : cos(180^o−α)= −cosα

Woda: Dzieki!

Basia: Cześć Eto Dobrze,że czuwasz