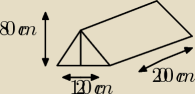
Bryły - graniastosłupy . marta: 1.) W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy długości 8 cm, przekątna ściany bocznej jest nachylona do podstawy pod kątem o mierze 60* (stopni). Oblicz objętość i pole powierzchni tego graniastosłupa. 2.) Oblicz: a) Iie powietrza mieści się w namioscie, b) jaką powierzchnię ma podłoga, a jaką ściany (przód, tył i boki). − RYSUNEK JEST DO 2 ZAD. !

raffels: Zadanie 1 V=Pp*H

	a2√3		64√3
Pp=		=		=16√3
	4		4

Na rysunku widok ściany bocznej, trójkąt prostokątny jest połową trójkąta równobocznego o podstawie 16, natomiast H jest wysokością tego trójkąta, zatem

	2a√3
H=		=U{16√3{2}=8√3
	2

Możemy liczyć objętość V=16√3*8√3=16*8*3=384cm³ Pc=2*Pp+3*Psb Ściana boczna jest prostokątem, którego wymiary już mamy, zatem Pc=2*16√3+3*8*8√3=32√3+192√3=224√3cm² Zadanie 2 Namiot jest graniastosłupem o podstwie trójkąta, mamy wszystkie dane do policzenia jego objętości

	1
V=		*120*80*200=120*80*100=960000cm3
	2

wejście to trójkąt, jego pole można łatwo policzyć

	1
Pw=		*120*80=60*80=4800cm2
	2

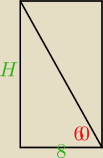
podłoga to prostokąt o wymiarach 120X200, zatem Ppodłogi=120*200=24000cm² pozostałe ściany są prostokątami przystającymi, jeden wymiar już mamy, czyli 200cm, drugi policzymy korzystając z twierdzenia pitagorasa 60²+80²=x² 3600+6400=x² 10000=x² x=100 zatem ściana to prostokąt o wymiarach 200X100, czyli: Ps=100*200=20000cm²