równanie mat-fiz: Wyznacz te wartości parametru k dla których równanie x⁴−10x²+k=0 ma cztery rozwiązania z których można utworzyć ciąg arytmetyczny. Dla wyznaczonej wartości k podaj te rozwiązania

Eta: Odp: k=9 , x∊{−3,−1,1,3}

Janek191: x⁴ − 10 x² + k = 0 x² = t t² − 10 t + k = 0 Δ = 100 − 4k > 0 ⇒ k < 25 więc t = U{10 − 2√25 − k{2} = 5 − √25 − k lub t = 5 + √25 − k zatem x² = 5 − √25 − k lub x² = 5 + √25 − k x = − √5 − √25 − k lub x = √5 − √25 − k lub x = −√5 + √25 − k lub x = √5+√25−k

Janek191: Zapomniałem o ciągu arytmetycznym

Eta:

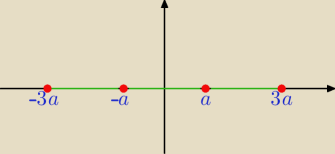
Eta: k<25 Ze względu na parzystość wielomianu po lewej stronie równania rozwiązania ułożą się symetrycznie : −3a, −a, a, 3a −−− tworzą ciąg arytmetyczny o różnicy 2a zatem równanie przybiera postać: (x+3a)(x−3a)(x+a)(x−a)=0 (x²−9a²)(x²−a²)=0 x⁴−10a²x²+9a⁴=0 i x⁴−10x²+k=0 to a²=1 więc k= 9 x⁴−10x²+9=0 ⇒(x²−9)(x²−1)=0 ⇒ x= −3 ,x=3 , x= −1, x=1 tworzą ciąg arytmetyczny: −3,−1, 1,3 lub 3,1,−1,−3

mat-fiz: Dzięki Eta