anulka: Punkty A=(4, -1) i B=(3,4) sa wierzcholkami trojkata rownoramiennego ABC, w ktorym
I AB I = I AC I . Wysokosc AD zawarta jest w prostej o rownaniu y= -x+3,
a) wyznacz wspolrzedne pkt. C
b) oblicz pole i obwod trojkata ABC
12 lis 19:27
M:
11 maj 17:05
Miś Uszaty:
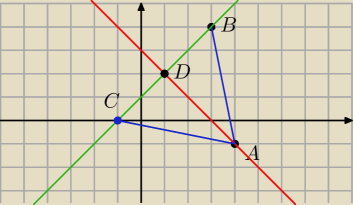
A=(4,−1) B=(3,4)
|AB|=
√(3−4)2+(4−(−1))2=
√26
|AC|=
√26
Równanie prostej prostopadłej do prostej AD i przechodzącej przez punkt B
m
1=1
y=1(x−3)+4
y=x−3+4
y=x+1
Współrzędne punktu D
x+1=−x+3
2x=2
x
D=1
y=x+1
y
D=1+1=2
D=(1,2)
Wpółrzedne punktu C (symetrycznego do punktu (B) względem prostej y=−x+3)
x
B+X
C=2x
D
x
C= 2x
D−x
B
x
C=2*1−3
x
C=−1
y
C=2y
d−y
B
y
C= 2*2−4
y
C=0
C=(−1,0)
Punkt C ma współrzene C=(−1,0)
|BC|=
√(−1−3)2+(0−4)2
|BC|=√32=4√2
Ob=2*√26+4√2
ob=2√26+4√2
A=(4,−1) B=(3,4) c=(−1,0)
| | 1 | |
P= |
| |(xB−xA)(yC−yA)−(yB−yA)(xC−xA)| |
| | 2 | |
| | 1 | |
P= |
| |(3−4)(0+1)−(4+1)(−1−4)| |
| | 2 | |
P=U[1{2}|(−1)+25|
11 maj 18:49
 A=(4,−1) B=(3,4)
|AB|=√(3−4)2+(4−(−1))2=√26
|AC|=√26
Równanie prostej prostopadłej do prostej AD i przechodzącej przez punkt B
m1=1
y=1(x−3)+4
y=x−3+4
y=x+1
Współrzędne punktu D
x+1=−x+3
2x=2
xD=1
y=x+1
yD=1+1=2
D=(1,2)
Wpółrzedne punktu C (symetrycznego do punktu (B) względem prostej y=−x+3)
A=(4,−1) B=(3,4)
|AB|=√(3−4)2+(4−(−1))2=√26
|AC|=√26
Równanie prostej prostopadłej do prostej AD i przechodzącej przez punkt B
m1=1
y=1(x−3)+4
y=x−3+4
y=x+1
Współrzędne punktu D
x+1=−x+3
2x=2
xD=1
y=x+1
yD=1+1=2
D=(1,2)
Wpółrzedne punktu C (symetrycznego do punktu (B) względem prostej y=−x+3)