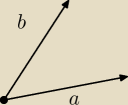
Rozpatrujemy 2 wektory zaczepione w tym samym punkcie (wektor a i b) cerisier: Rozpatrujemy 2 wektory zaczepione w tym samym punkcie (wektor a i b) Zaznacz wszystkie rozwiązania pa + qb gdy p i q są dowolnymi liczbami rzeczywistymi, oraz p+q = 1 oraz p>0 i q>0 Uzasadnij odpowiedzi. Podejrzewam, że tutaj powinna być wykorzystana nierówność Schwartza, ale nie mam pojęcia jak to ugryźć

cerisier:

Pytający: Mamy: p∊(0,1), q=1−p, pa+qb=pa+(1−p)b=b+p(a−b) Czyli koniec wektora pa+qb (zaczepionego w tym samym punkcie co wektory a, b) leży na odcinku łączącym końce wektorów a i b z wyłączeniem samych końców tych wektorów (bo p≠0 i p≠1).