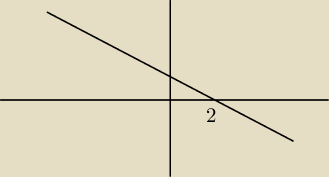
monotoniczność Toem: Witam, jak określić monotoniczność

	4
f(x)=x+
	x2

	8
f'(x)1−
	x3

wiem że miejsce zerowe to x=2 dziedzina R\{0} a znak przy najwyższym współczynniku to −1. więc rysuję od prawej strony zaczynając od dołu: czyli (−∞,0) rosnąca (0,2) rosnąca (2,∞) malejąca dobrze?

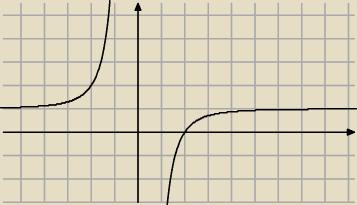Basia: to jest wykres Twojej pochodnej

Toem: hmm ale dlaczego ona tak wygląda? jak ja mam do tego dojść na sprawdzianie? tam nie mam generatorów funkcji

Basia: tak będzie łatwiej

	x3−8
f'(x) =
	x3

x∊(−∞;0) ⇒ x³−8 <0 ∧ x³<0 ⇒ f'(x)>0 x∊(0,2)⇒ x³−8<0 ∧ x³>0 ⇒ f'(x)<0 x∊(2;+∞) ⇒ x³−8>0 ∧ x³>0 ⇒ f'(x)>0

Toem: wielkie dzięki,