G Student: Wyznaczyć przedziały wypuklosci i wkleslosci funckji

ex
	nie potrafię rozwiązać
x+2

iteRacj@: jaką masz pierwszą i druga pochodną?

Student:

ex(x+2)+ex
	to pierwsza
(x+2)2

Student:

ex(x2+4x+4)+ex
	to druga
(x+2)4

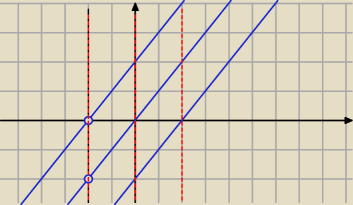
Basia: x≠−2

	ex(x+2) − 1*ex		ex*(x+1)		x+1
f'(x) =		=		= ex*
	(x+2)2		(x+2)2		(x+2)2

	x+1		1*(x+2)2 − 2(x+2)(x+1)
f"(x) = ex*		+ ex*		=
	(x+2)2		(x+2)4

	(x+1)(x+2)2 + (x+2)2− 2x(x+2)(x+1)
ex*		=
	(x+2)4

	(x+2)[(x+1)(x+2) + (x+2) −2x(x+1)]
ex*		=
	(x+2)4

	x2+3x+2+x+2 −2x2−2x
ex*		=
	(x+2)3

	−x2+2x		−x(x−2)
ex*		= ex*		=
	(x+2)3		(x+2)3

	ex
−		*[x(x−2)(x+2)]
	(x+2)4

znak drugiej pochodnej zależy tylko od znaku wyrażenia x(x−2)(x+2)

	ex
bo −		jest stale ujemny
	(x+2)4

m.zerowe x=−2 x=0 x=2 x∊(−∞;−2) ⇒ f"(x)>0 ⇒ f jest wypukła x∊(−2;0) ⇒ f"(x)<0 ⇒f jest wklęsła x∊(0,2) ⇒ f"(x)>0 ⇒ f jest wypukła x∊(2;+∞) ⇒ f"(x)<0 ⇒ f jest wklęsła

	1		e2
w punktach (0;		) i (2;		) są punkty przegięcia
	2		4

w punkcie −2 nie bo −2∉D_f

iteRacj@: pierwsza pochodna

ex(x+2)−ex
(x+2)2

Student: Basiu dlaczego w 1 pochodnie jest (x+1)?

Basia: wyłączam e^x przed nawias i w nawiasie mam (x+2−1) = (x+1)

Student: A w 2 pochodnej w drugiej linijce skąd 2 przed dwoma nawiasami?

Basia: [(x+2)²]' =2(x+2)*1 = 2(x+2)

Student: A ten + w drugiej linijce jest dlatego ze masz na uwadze korzystanie później ze wzoru na mnożenie pochodnych?

Basia: nie wiem o który plus chodzi

Student: Między ulamkami

Student: Jak liczysz drugą pochodną

Basia: f'(x) jest iloczynem e^x*ułamek f"(x) = (e^x)'*ułamek + e^x*(ułamek)'

Student: Tal dokładnie o ten plus mi chodzi, skąd on się bierze. Nie rozumiem tej drugiej pochodnie

Basia: no napisałam przecież skąd się bierze; liczę pochodną iloczynu (fg)'=f'g + fg'

Student: Teraz rozumiem