równanie miejsca geometrycznego
jojo: Znajdź równanie miejsca geometrycznego punktów P(x,y) spełniających warunek: suma kwadratów
odległości punktu P od punktów:
a) A(−1,2) i B(3,2) jest równa 16
b) A(2,−3), B(0,1) i C(−2,−1) jest równa 19
c) A(2,−4), B(−1,0), C(0,4) i D(3,0) jest równa 50.
25 sty 15:52
Mila:
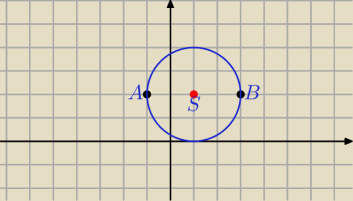
a) A(−1,2) i B(3,2) jest równa 16
|AB|=4 to będzie okrąg
P(x,y) taki punkt , że:
|AP|
2+BP|
2=16⇔
(x+1)
2+(y−2)
2+(x−3)
2+(y−2)
2=16
po wykonaniu działań i redukcji:
x
2−2x+y
2−4y=−1
(x−1)
2−1+(y−2)
2−4=−1
(x−1)
2+(y−2)
2=4
S=(1,2), r=2
25 sty 17:45
Mila:
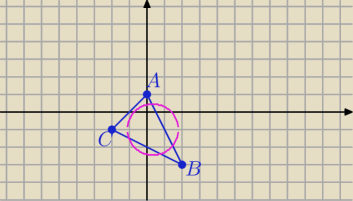
b) A(2,−3), B(0,1) i C(−2,−1) jest równa 19
P(x,y) taki punkt , że:
(x−1)
2+(y+3)
2+x
2+(y−1)
2+(x+2)
2+(y+1)
2=19⇔
3x
2+2x+3y
2+6y=3 /:3
| | 1 | | 1 | |
(x+ |
| )2− |
| +(y+1)2−1=1 |
| | 3 | | 9 | |
okrąg
Posprawdzaj rachunki.
25 sty 17:58
jojo: Wielkie dzięki

25 sty 21:59
Mila:

25 sty 22:08
ola: a w podpunkcie c wyszło mi tak:
A(2,−4), B(−1,0), C(0,4) i D(3,0) jest równa 50
(x−2)
2+(y+4)
2+(x+1)
2+y
2+x
2+(y−4)
2 (x−3)
2+y
2=50
(4x)
2−8x+4y
2=4 /:4
x
2−2x+y
2=1
Jak to dalej rozpisać


26 sty 10:36
iteRacj@:
wcześniejszych rachunków nie sprawdzałam
x2−2x+y2=1
x2−2*1*x+1−1+y2=1
(x2−2*1*x+12)−1+y2=1 //+1
(x2−2*1*x+12)+y2=1+1
(x−1)2+y2=2
czyli (x−1)2+(y−0)2=2 okrąg o środku (1,0) i promieniu √2
26 sty 11:12
jojo: Świetnie. Dzięki

26 sty 12:49
 a) A(−1,2) i B(3,2) jest równa 16
|AB|=4 to będzie okrąg
P(x,y) taki punkt , że:
|AP|2+BP|2=16⇔
(x+1)2+(y−2)2+(x−3)2+(y−2)2=16
po wykonaniu działań i redukcji:
x2−2x+y2−4y=−1
(x−1)2−1+(y−2)2−4=−1
(x−1)2+(y−2)2=4
S=(1,2), r=2
a) A(−1,2) i B(3,2) jest równa 16
|AB|=4 to będzie okrąg
P(x,y) taki punkt , że:
|AP|2+BP|2=16⇔
(x+1)2+(y−2)2+(x−3)2+(y−2)2=16
po wykonaniu działań i redukcji:
x2−2x+y2−4y=−1
(x−1)2−1+(y−2)2−4=−1
(x−1)2+(y−2)2=4
S=(1,2), r=2
 b) A(2,−3), B(0,1) i C(−2,−1) jest równa 19
P(x,y) taki punkt , że:
(x−1)2+(y+3)2+x2+(y−1)2+(x+2)2+(y+1)2=19⇔
3x2+2x+3y2+6y=3 /:3
b) A(2,−3), B(0,1) i C(−2,−1) jest równa 19
P(x,y) taki punkt , że:
(x−1)2+(y+3)2+x2+(y−1)2+(x+2)2+(y+1)2=19⇔
3x2+2x+3y2+6y=3 /:3




