BRYŁY Jola: W ostrosłupie prawidłowym sześciokątnym krawędź podstawy ma długość a, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz promień kuli: a) opisanej na tym ostrosłupie b) wpisanej w ten ostrosłup Prosze o wskazówki i możliwy rysunek

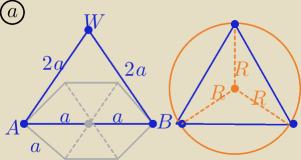
Eta: Przekrój jest trójkątem równobocznym o boku długości 2a

	2a√3
to promień kuli opisanej R=
	3

Jola: Bardzo dziękuję za rozwiązanie <3

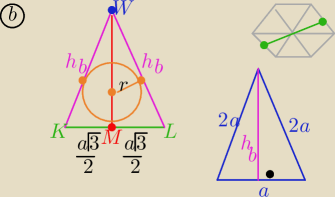Eta: Kula wpisana w ostrosłup jest styczna do podstawy i do wszystkich ścian bocznych zatem przekrojem ostrosłupa jest trójkąt KLW o ramionach h_b i podstawie 2h_Δ równobocznego podstawy to długość |KL|= a√3 długość h_b wyliczamy z twierdzenia Pitagorasa w ścianie bocznej( niebieski rys.)

	a2		√15a
hb=√4a2−		=
	4		2

Długość promienia można obliczyć ze wzoru P=rp h=|WM|= √(15a²/4)− (3a²/4)= a√3 P(KLW)= ..= 3a²

	3a2		3a		a√3(√5−1)
r=		=		= ...
	√15a+√3a		√3(√5+1)		4