BRYŁY OBROTOWE Jola: Dany jest trójkąt równoramienny, w którym kąt przy podstawie ma miarę 30, a wysokość opuszczona na podstawę jest równa 1. Oblicz objętość i pole powierzchni bryły otrzymanej przez obrót tego trójkąta wokół: a) jego podstawy b) jego ramienia Proszę o pomoc wraz z rysunkiem

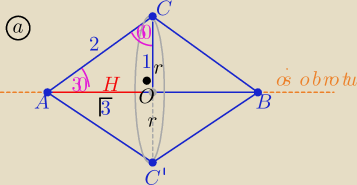
Eta: a) Bryła składa się z dwóch przystających stożków sklejonych podstawami wymiary stożków r=h_Δ=1 i H= √3

	2
V(bryły) 2*V(stożka) =		*π*√3
	3

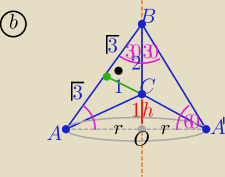Eta: Bryła składa się ze stożka AA^'B i wydrążonego w podstawie stożka AA^'C trójkąt AA^'B jest równoboczny o boku długości 2√3 wymiary dużego stożka : r=√3 i H=|OB|=2+1=3 wymiary małego( wydrążonego stożka) : r=√3 i h= 1 V(bryły )=V(dużego stożka )− V(małego stożka)

	1		1		1
V(bryły)=		πr2*H−		πr2*h =		πr2(H−h)=.....=2π [j3]
	3		3		3

Jola: Dzięki bardzo

Eta: Na zdrowie ....