Planimetria zenek: Trapez równoramienny którego pole wynosi 28√3 , opisano na okręgu o promieniu długości 2√3.Oblicz długość boków tego trapez.

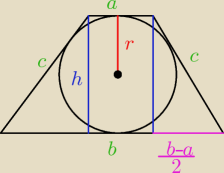
Godzio: okręg wpisany w trapez : a+b = 2c h=2r = 4√3

	a+b
P = 28√3 =		*h
	2

28√3 = 2√3(a+b) 14 = a+b a+b=2c a+b=14 14=2c c=7 a+b = 14 => b=14−a

	b−a
(		)2 + h2 = c2 /*4
	2

(b−a)² + 192 = 196 (14−2a)² = 4 /√ 14 − 2a = 2 −2a = −12 a = 6 b+6=14 b = 8