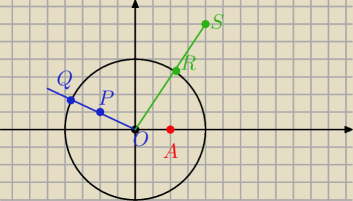
 jak rozumiesz odległość punktu od okręgu?
długość którego odcinka jest odległością P od okręgu?
to samo odnośnie S
jak rozumiesz odległość punktu od okręgu?
długość którego odcinka jest odległością P od okręgu?
to samo odnośnie S
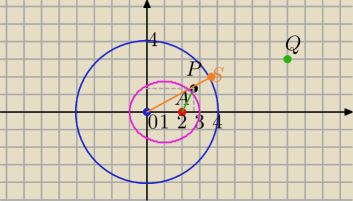 A=(2,0)
P(x,y)− punkt jednakowo odległy od okręgu i punktu A.
Każdy punkt (Q ) leżący na zewnątrz okręgu będzie miał bliżej do okręgu niż do A.
Zatem szukane punkty leżą wewnątrz okręgu:
|AP|=√(x−2)2+y2 odległość P od punktu A
|PS|=4−√x2+y2
√(x−2)2+y2 =4−√x2+y2 /2
(x−2)2+y2=16−8√x2+y2+x2+y2
x2−4x+4+y2=16−8√x2+y2+x2+y2
−4x+4=16−8√x2+y2 /:4
−x+1=4−2√x2+y2
2√x2+y2=3+x /2
4*(x2+y2)=9+6x+x2
3x2−6x+4y2=9 szukana krzywa , przekształcamy do postaci kanonicznej
3*(x2−2x)+4y2=9
3*[(x−1)2−1]+4y2=9/:3
A=(2,0)
P(x,y)− punkt jednakowo odległy od okręgu i punktu A.
Każdy punkt (Q ) leżący na zewnątrz okręgu będzie miał bliżej do okręgu niż do A.
Zatem szukane punkty leżą wewnątrz okręgu:
|AP|=√(x−2)2+y2 odległość P od punktu A
|PS|=4−√x2+y2
√(x−2)2+y2 =4−√x2+y2 /2
(x−2)2+y2=16−8√x2+y2+x2+y2
x2−4x+4+y2=16−8√x2+y2+x2+y2
−4x+4=16−8√x2+y2 /:4
−x+1=4−2√x2+y2
2√x2+y2=3+x /2
4*(x2+y2)=9+6x+x2
3x2−6x+4y2=9 szukana krzywa , przekształcamy do postaci kanonicznej
3*(x2−2x)+4y2=9
3*[(x−1)2−1]+4y2=9/:3
| 4y2 | ||
(x−1)2−1+ | =3 | |
| 3 |
| 4y2 | ||
(x−1)2+ | =4 /:4 | |
| 3 |
| (x−1)2 | y2 | ||
+ | =1 elipsa | ||
| 4 | 3 |