Wyznacz na prostych 3x + y − 4 = 0 i 2x − y − 4 = 0 punkty symetryczne względem zak15: Proszę o sprawdzenie Wyznacz na prostych 3x + y − 4 = 0 i 2x − y − 4 = 0 punkty symetryczne względem osi OX Z równania prostej 3x + y − 4 = 0 wyznaczyłem wektor prostopadły do tej prostej P[3,1], a następnie jego współrzędne odbiłem względem osi OX i wyszło mi P`[3,−1] drugie zrobiłem analogicznie. Dobrze

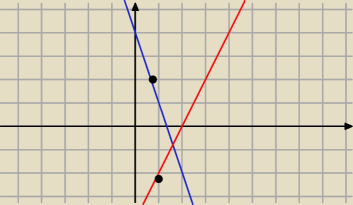
Basia: masz znaleźć punkt A∊K i punkt B∊l tak aby te punkty były symetryczne wzgl. OX A(x,y) B(x;−y) A(x, 2x−4) B(x, −3x+4) −(2x−4) = −3x+4 −2x+4 = −3x+4 x = 0 stąd A(0;−4) B(0;4)

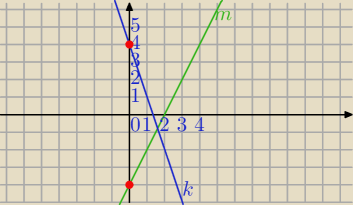
Mila: 3x + y − 4 = 0 i 2x − y − 4 = 0 k: y=−3x+4 i m: y=2x−4 A=(x,−3x+4)∊k A'=(x,2x−4)∊m Punkty symetryczne względem OX mają pierwsze wsp. jednakowe, a drugie są liczbami przeciwnymi. 3x−4=2x−4 x=0 y=4 A=(0,4) A'=(0,−4)

Mila: Jednomyślne

Basia: Cześć Milu Ładnie się spotkałyśmy.

Mila: cześć!

zak15: Dziękuję