wyznacz równanie stycznej zak15: Wyznacz równania stycznych do danego okręgu: x² + y² = 5, przechodzących przez punkt P(1, −2)

PW: Współrzędne punktu P spełniają równanie okręgu: 1²+(−2)²=5, mamy zatem poprowadzić styczną do okręgu przechodzącą przez punkt P należący do tego okręgu. Jest tylko jedna taka styczna − prostopadła do wektora SP^→, gdzie S oznacza środek okręgu, S=(0, 0), P=(1, −2) SP^→=[1,−2]. Dalej samodzielnie.

zak15: proszę o sprawdzenie: wychodzę z równanie A(x−x₀)+B(y−y₀)=0 i z tego po podstawieniu za A=1 B=−2 otrzymuję równie x−2y−5=0

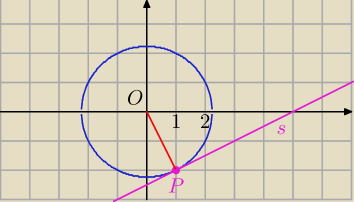
Mila: x²+y²=5 Prosta OP: O=(0,0), P=(1,−2)∊okręgu Styczna s: s⊥OP OP^→=[1,−2] x−1−2*(y+2)=0 s: x−2y−5=0 A w postaci kierunkowej:

	1		5
s: y=		x−
	2		2

Eta: Jeżeli punkt P(x_o,y_o) ∊ o: (x−a)²+(y−b)²=r² to styczna w punkcie P ma równanie: (x−a)(x_o−a)+(y−b)(y_o−b)=r² W tym przykładzie P(1,−2) ∊ o : x²+y²=5 bo 1²+(−2)²=5 zatem styczna ma równanie: x*1+y*(−2)=5 x−2y=5 −−− równanie stycznej ========

piotr: Równanie stycznej do krzywej f(x,y) = 0 w punkcie P(x_P, y_P)

	df(x,y)   (xP, yP) dx
y − yP = −		(x − xP)
	df(x,y)   (xP, yP) dy