Suma rodziny indeksowanej Julcia: Znajdź sumę U_n∊ℤ i przekrój ∩_n∊ℤ Jeśli zbiory A_n są równe A_n={(x,y)∊ℛ² : x<n*y}

kochanus_niepospolitus: 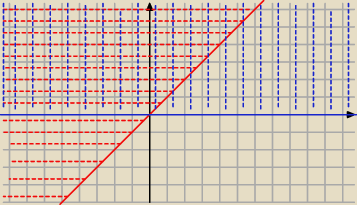A₁ A_∞ Więc jaka będzie suma tej rodziny zbiorów? A jaka część wspólna (uwaga ... wykresy funkcji y=x i y=0 NIE NALEŻĄ do zbiorów A₁ i A_∞

Julcia: A skąd ten niebieski wykres? przecież jeśli n dąży do nieskonczonosci to wykres powinien sie raczej kurczyć i iść do gory. czy nie?

Julcia: a nie dobra bład moj juz widze jednak dobrze

Julcia: tylko jak na koncu to wszystko formalnie zapisac jaka jest suma a jaki przekroj?

kochanus_niepospolitus:

	x		x
masz x < n*y ... więc y>		teraz limn−>∞		= 0
	n		n

kochanus_niepospolitus:

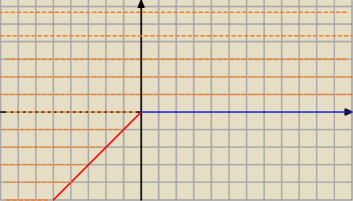
	⎧	y>0 ; dla x≥0
Un∊N An =	⎩	y>x ; dla x<0

Część wspólną sama spróbuj.

Julcia: dobra już rozumiem, dzięki wielkie

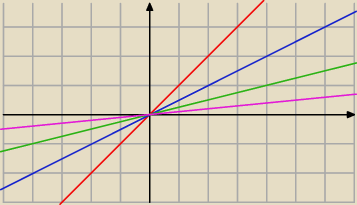
kochanus_niepospolitus: masz proste 'określające': F₁ F₂ F₄ F₁₀ czyli proste: y = x ; y = x/2 ; y = x/4 ; y= x/10

Julcia: tylko że w zadaniu było n∊ℤ. to chyba trochę robi róznice, czy nie?

Julcia: wtedy suma będzie chyba całe R² z wyjątkiem dodatniej osi x a przekruj pusty?

Julcia: przekrój*

Julcia: albo przkrój to ujemna oś x

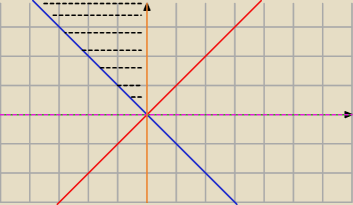
kochanus_niepospolitus: nie bardzo rozumiem jak może być zbiór A₋₄ dla mnie to jest idiotyczny indeks Jeżeli weźmiemy pod lupę wszystkie Całkowite liczby n, to mamy: y=x (czyli A₁ to nad prostą) y=−x (czyli A₋₁ to nad prostą) y=0 i y=0 (czyli A_∞ i A_−∞ to ponad osią OX) Pozostaje nam jeszcze A₀ czyli wszystko 'na lewo' od y=0 Zaznaczony przedział (bez prostej i prostej) to będzie część wspólna. Sumą będzie wszystko poza analogicznym trójkątem w IV ćwiartce.

Pytający: Kochanus, zapomniałeś o zmianie znaku nierówności przy dzieleniu przez liczbę ujemną. Wg mnie tak jak mówi Julcia: U_n∊ℤ={(x,y)∊ℛ²: y≠0 ∨ (y=0 ∧ x<0)} ∩_n∊ℤ={(x,y)∊ℛ²: y=0 ∧ x<0}

kochanus_niepospolitus: faktycznie ... no to skoro mamy: y>x oraz y<−x to sumą będzie R² /{(0,0)} (co załatwiają nam A_∞ i A_−∞) (bo (0,0) to jest jedyny punkt wspólny dla każdej z tych prostych) natomiast częścią wspólną będzie zbiór pusty bo powyższe zbiory (A_∞ i A_−∞) są rozłączne.

kochanus_niepospolitus: tfu tfu ... sumą będzie R² / {<0;+∞),0} czyli z wyjątkiem półprostej: y=0 dla x≥0 czyli tak jak napisałeś. Ale z przekrojem się nie zgodzę.

kochanus_niepospolitus: dobra ... z przekrojem też się zgadzam