Stereometria UczącySię: 1)Podstawą ostrosłupa o wysokości h jest trapez równoramienny o podstawach a i b i ramieniu c. Płaszczyzną równoległą do podstawy przekrojono ten ostrosłup na dwie części o równych objętościach. Oblicz pole przekroju 2) Na półsferze o promieniu r leżą dwa styczne do siebie okręgi o promieniu R. Wyznacz największą odległość między dwoma punktami należącymi do tych okręgów. Proszę o jakieś podpowiedzi lub nakreślenie sytuacji a nie gotowe rozwiązania

Basia:

	a+b
Ptrapezu1=		*h
	2

	a+b
Vostr.1 =		*h
	2

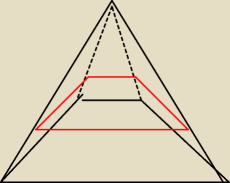
V₁ to objetość tego ostrosłupa "na górze"

	1
V1=		V
	2

	V1		1
ostrosłupy są podobne w skali k3=		=
	V		2

	1
k =
	3√2

podstawy tych ostrosłupów są podobne w tej samej skali czyli

	1		a+b
Pprzekroju = k2*Ptrapezu1 =		*		*h
	3√4		2

Basia:

	1
razy		oczywiście przy każdym V i V1
	3

UczącySię:

	(a+b) * √4*c2−(a−b)2
Mam wynik, wynosi on:
	3√22 * h

A tutaj chyba taki nie wyszedł. Aczkolwiek Twoja metoda chyba jest poprawna