Dany jest trójkąt prostokątny, w którym promień okręgu wpisanego jest równy 2, a
pp1:
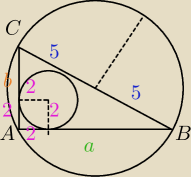
Dany jest trójkąt prostokątny, w którym promień okręgu wpisanego jest równy 2, a opisanego
5. Oblicz długości boków i sumę sinusów kątów ostrych w tym trójkącie.
Skorzystałem z własności trójkąta wpisanego (bok AB podpisałem: 2 (tam gdzie r) i a−2,
analogicznie AC)
I miałem:
|AC|=a+b−2r
10=a+b−4
a+b=14
a=14−b
Podstawiłem do twierdzenia Pitagorasa, ale potem z równania kwadratowego wyszły mi dwa
przypadki, gdzie a=6,b=8 oraz a=8,b=6.
Dobrze zrobiłem czy popełniłem jakiś błąd? Nie mam odpowiedzi do tego zadania, więc nie mam jak
sprawdzić.
