Podstawą ostrosłupa jest romb, w którym krawędź podstawy jest równa 6 i krótsza ew: Podstawą ostrosłupa jest romb, w którym krawędź podstawy jest równa 6 i krótsza przekątna 8. Ściany boczne ostrosłupa są nachylone do podstawy pod kątem 45°. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

===: a jakiś wkład własny?

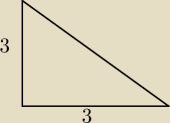
ew: Obliczyłem pole podstawy z wzoru na przekątne (drugą przekątną obliczyłem najpierw licząc pole trójkąta w podstawie, a potem z tw. Pit przeciwprostokątną). Druga przekątna wyszła mi 4√5, więc pole=16√5 Z obrazka ten kąt 45 stworzył mi z wysokością trójąt 90,45,45, a za podstawę przyjąłem 1/2 krawędzi bocznej, więc boki wyszły mi 3,3,3√2 Teraz nie wiem co dalej. Objętość mogę obliczyć, ale pole boczne nie wiem czy ta przeciwprostokątna jest wysokością trójkąta bocznego i czy z tego mogę obliczyć pole boczne

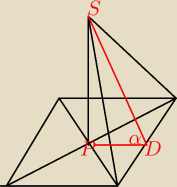
Basia: tak; SD=3√2 jest wysokością ściany bocznej, bo jest prostopadła do krawędzi podstawy inaczej <PDO nie byłby kątem nachylenia ściany bocznej do podstawy czyli

	1
Pb = 4*		*3*3√2
	2

===: początek ok ....ale ten trójkąt z wysokością ostrosłupa juz nie

Basia: wow, przecież to romb

===: ...policzyć z podobieństwa trójkątów

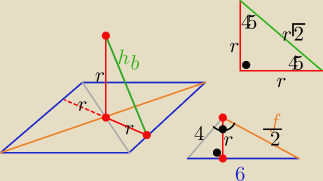
Eta: r −− długość promienia okręgu wpisanego w romb z tw. Pitagorasa (f/2)²= 6²−4² ⇒ f /2= 2√5

	4*f/2
to r=H=		= ................
	6

h_b= r√2= ............ V= ........... P_c= P_p+4*U{1/2}*6*h_b=............. dokończ

Basia: Eto skąd wiadomo, że odcinek poprowadzony z wierzchołka tego ostrosłupa do spodka promienia r będzie prostopadły do krawędzi podstawy? Nie widzę z czego to wynika.

===: ... z definicji kąta dwuściennego