Przedziały monotoniczności Czarek: Wyznacz przedziały monotoniczności i ekstrema lokalne

	2
lnx−x−
	x2

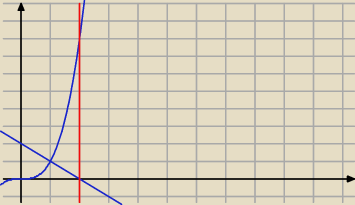
Basia: x>0 x∊(0;+∞)

1

2

1

4

x2−x3+4

−x3+x2+4

f'(x) =

−1+

*2x =

−1+

=

=

=

x

x4

x

x3

x3

x3

−(x3−x2−4)		−(x−2)(x2+x+2)
	=
x3		x3

f'(x)=0 ⇔ x−2=0 ⇔ x=2 (bo x²+x+2>0 dla każdego x∊D)

	−(x−2)		−x+2
znak pochodnej zależy od znaku funkcji y=		=		(wykres)
	x3		x3

x∊(0;2)⇒ f'(x)>0 ⇒ f rośnie x∊(2,+∞) ⇒ f'(x)<0 ⇒ f maleje mamy minimum lokalne dla x=2

	2
fmin=f(2) = (ln2)−2−		= −2,5 + ln(2)
	4

Czarek: Dziękuje bardzo

Czarek: A pomogła byś jeszcze z jednym przykładem?

Basia: napisz

Czarek: f(x)=arctg(x−1)+ln(2x)

Basia: 2x>0 x>0 x∊(0;+∞)

	1		1		1		1
f'(x) =		*1 +		*2 =		+		=
	1+(x−1)2		2x		1+x2−2x+1		x

1		1		x+x2−2x+2		x2−x+1
	+		=		=
x2−2x+2		x		x(x2−2x+2)		x(x2−2x+2)

łatwo sprawdzić,że y=x²−x+1>0 dla każdego x∊D (Δ=1−4<0) czyli pochodna nie ma miejsc zerowych czyli nie będzie żadnych ekstremów lokalnych y=x²−2x+2>0 dla każdego x∊D (Δ=4−8<0) znak pochodnej zależy tylko od funkcji y=x a ta również w D jest stale dodatnia czyli funkcja jest rosnąca w całej swojej dziedzinie

Basia: w liczniku x²−x+2, ale to niczego nie zmienia

Czarek: Jeszcze raz dziękuje