Wykaz
Janko:
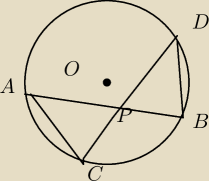
Wykaż,że trójkąty ACP i BDP są podobne oraz uzasadnij,że |PA|*|PB|=|PC|*|PD|.Oblicz promień
okręgu,jeśli |AP|=5,|PB|=2,|CP|=1,i∡CBD=150 stopni
23 sty 21:56
===:
Podobieństwo trójkątów na zasadzie kkk
23 sty 22:06
Basia:
kąty ACD i ABD są oparte na tym samym łuku ⇒
|<ACD|=|<ABD}|
kąty APB i BDP są wierzchołkowe ⇒
|<APB|=|<BDB|
na mocy cechy kk tr.ACD~tr.ABD
stąd
|PA|*|PB| = |PC|*|PD|
23 sty 22:08
Janko: a nie mozna np :
∡PAC=∡BPD −> wierzcholkowe
∡PBD=∡PAC (naprzemian albo naprzeciwlegle nie pamietam)
zatem ΔPAC~ΔPBD? (KK)
23 sty 22:16
Janko: I potem z proporcji wyliczyc PD czyli 10,dodac do tego CP czyli 11 i podstawic pod twierdzenie
sinusow majac 150stopni i bok 11 zeby wyliczyc R?
23 sty 22:22
Janko: wydaje mi sie ze do momentu wyliczenia boku z proporcji jest tylko dobrze xd
23 sty 22:24
Basia:
nie można; to nie są katy naprzemianległe
odcinki AC i BD nie są równoległe
PBD i PAC mają równe miary bo są wpisane i oparte na tym samym łuku
potem masz
5*2=1*|PD|
|PD|=10
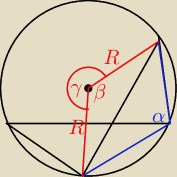
α=150
γ=300 (kąt środkowy oparty na tym samym łuku co wpisany α)
β=60
czyli tr.COD jest równoboczny czyli R=11
rysunek nie za bardzo przystaje do rzeczywistości jak widać
23 sty 22:45
Janko: Dziekuje
23 sty 22:52
 Wykaż,że trójkąty ACP i BDP są podobne oraz uzasadnij,że |PA|*|PB|=|PC|*|PD|.Oblicz promień
okręgu,jeśli |AP|=5,|PB|=2,|CP|=1,i∡CBD=150 stopni
Wykaż,że trójkąty ACP i BDP są podobne oraz uzasadnij,że |PA|*|PB|=|PC|*|PD|.Oblicz promień
okręgu,jeśli |AP|=5,|PB|=2,|CP|=1,i∡CBD=150 stopni
 nie można; to nie są katy naprzemianległe
odcinki AC i BD nie są równoległe
PBD i PAC mają równe miary bo są wpisane i oparte na tym samym łuku
potem masz
5*2=1*|PD|
|PD|=10
α=150
γ=300 (kąt środkowy oparty na tym samym łuku co wpisany α)
β=60
czyli tr.COD jest równoboczny czyli R=11
rysunek nie za bardzo przystaje do rzeczywistości jak widać
nie można; to nie są katy naprzemianległe
odcinki AC i BD nie są równoległe
PBD i PAC mają równe miary bo są wpisane i oparte na tym samym łuku
potem masz
5*2=1*|PD|
|PD|=10
α=150
γ=300 (kąt środkowy oparty na tym samym łuku co wpisany α)
β=60
czyli tr.COD jest równoboczny czyli R=11
rysunek nie za bardzo przystaje do rzeczywistości jak widać