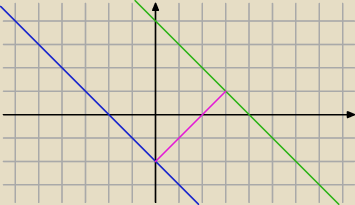
analityczna Agata: Oblicz odległość między prostymi równoległymi k i l k: x+y +2 = 0 l: x+y − 4 =0

===:

Basia: wybierz sobie byle który punkt na jednej i oblicz jego odległość od drugiej

pl: k: x + y + 2 = 0 l: x + y − 4 = 0 wybierz dowolny punkt z jednej prostej i zbadaj odleglosc tego punktu od drugiej prostej. np. k: weźmy za x = 0, wtedy 0 + y + 2 = 0 −−> y = − 2 mamy punkt (0,−2) i ze wzoru na odleglosc

	|Ax+By+C|		|1*0 + 1 * (−2) + (−4)|
d =		=
	√A2+B2		√12+12

	|−6|		6		6√2
d =		=		=		= 3√2
	√2		√2		2

Agata: oki, a jak będe miała k: x+6 = 0 l: 5x−10 = 0 ?

===: narysuj i zobaczysz

Agata: oki, wyszło mi 8 , ale w jaki sposób to narysować?

Eta: k: Ax+By+C₁=0 p: Ax+By+C₂=0

	|C1−C2|
k∥p ⇒ d=
	√A2+B2

w tym przykładzie

	|2+4|		6
d=		=		=3√2
	√2		√2

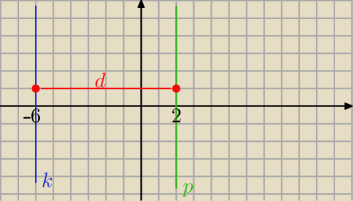
Eta: k: x=6 p: x= 2 d=10

Agata: ten przykład mi jeszcze nie wychodzi k: 2x−y +3=0 l: −3x + 1,5y −2 =0

Eta: k: 2x−y+3=0 C₁=3

	3
l: −3x+		y−2=0 /*(−2)
	2

6x−3y+4=0 /:3

	4
2x−y+		=0 C2= 4/3
	3

	|C1−C2|
d=		=............
	√22+(−1)2

dokończ

iteRacj@: 2x−y +3=0 pomnóż stronami przez (−1,5) i zastosuj wzór Ety z 20:46