całka podwójna Zaben1337: Wprowadzając współrzędne biegunowe obliczyć całkę podwójną ∬y dx dy D: x²+y²−2x<=0 y>=0 dochodzę do momentu gdy powstaje mi całka 8/3 ∫sin⁴φ dφ, od −pi/2 do pi/2, zastanawiam się czy to dobrze, bo całka wygląda na dość trudną.

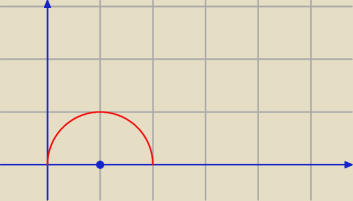
Basia: na rysunku jest obszar całkowania x²+y²−2x≤0 (x−1)²−1+y²≤0 (x−1)²+y²≤1 x=rcosφ y=rsinφ

	cosφ −rsinφ sinφ rcosφ
J= det		= rcos2φ+rsin2φ=r

	π
0≤φ≤
	2

r²cos²φ+r²sin^φ−2rcosφ≤0 r²−2rcosφ≤0 /:r r − 2cosφ≤0 0≤r≤2cosφ ₀∫^π/2dφ₀∫^2cosφr²sinφdr =

	r3
0∫π/2dφ [		sinφ]02cosφ =
	3

	8cos3φ*sinφ
0∫π/2		dφ=
	3

8
	0∫π/2cos3φsinφ dφ
3

t=cosφ dt = −sinφdφ

	8		8		1		2
=−		1∫0t3dt = −		*		*(04−14) =
	3		3		4		3

jeżeli się nie pomyliłam

jc: Proponuję przesunąć początek układu biegunowego. (x−1)²+y²≤1, y≥0 x = 1+r cos φ y = r sin φ J = r

	1		2
∫∫ydxdy = ∫0π dφ ∫01 r sin φ rdr =		∫0π sin φ dφ =
	3		3

Lech: Bardzo dobra metoda @jc ! !