Pomóżcie proszę w tym zadaniu Eli: Wyznacz równanie prostej zawierającej dwusieczną: a) kąta między prostymi 9x + 2y + 1 = 0 i 7x – 6y – 3 = 0 b) kąta między prostymi x + 2y – 5 = 0 i 3x − 6y + 2 = 0, do wnętrza którego należy punkt (2,−1).

Lech: Skorzystaj ze wzoru na odleglosc punktu P(x,y) od prostych , odleglosci te sa jednakowe !

Basia: ad.a każdy punkt leżący na dwusiecznej kąta jest równoodległy od ramion tego kąta stąd jeżeli P(x,y) k: 9x+2y+1=0 i l: 7x−6y−3=0 musi być d(P,k) = d(P,l)

|9x+2y+1|		|7x−6y−3|
	=
√92+22		√72+(−6)2

|9x+2y+1|		|7x−6y−3|
	=
√85		√85

|9x+2y+1|=|7x−6y−3| 9x+2y+1=7x−6y−3 lub 9x+2y+1=−7x+6y+3 2x+8y+4=0 lub 16x−4y−2=0 x+4y+2=0 lub 8x−2y−1=0

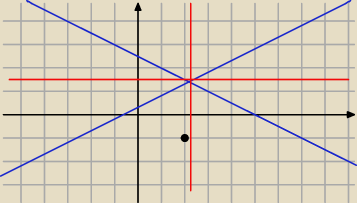
Basia: w (b) napisz równania dwusiecznych tak jak w (a) i pomóż sobie rysunkiem formalnie też to można zrobić