równanie elipsy
pata: Znaleźć równanie elipsy o ogniskach F1 = (1,1), F2 = (9,1), która przechodzi przez punkt P =
(5,−2).
Znalazłam środek tej elipsy. S = (5,1), czyli połowę równania. nie wiem jednak jak znaleźć
długości osi elips a i b.
22 sty 23:13
Basia:
|F1P|+|F2P|=2a (2a − oś wielka elipsy)
c= √b2−a2 c=|F1F2| 2b − oś mała elipsy
22 sty 23:38
pata: oś wielka mi wyszła 2a =10
22 sty 23:53
pata: jak wyliczyć oś małą? obliczyłam długość |F1F2| wyszło 8. czyli c=8
22 sty 23:54
Basia: podaję sposób, bo nie mam już czasu sprawdzać obliczeń
c = √b2−a2
8 = √b2−52
64 = b2−25
b2 = 89
b = √89
23 sty 00:00
pata: tylko, że b ma wyjść 3
23 sty 00:01
iteRacj@: Ogniskowa elipsy jest to odległość pomiędzy ogniskami. Jest ona równa 2c.
|F1F2| = 2c = 8 ⇒ c=4
Zależność pomiędzy półogniskową a osiami przedstawia wzór:
c2 = a2 − b2
b2 = a2 − c2
c=4, a=5
b2 = 52 − 42 = 32, b>0
b=3
23 sty 13:33
Mila:
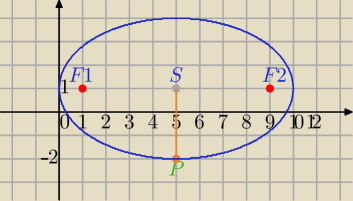
S=(5,1)
|PS|=b=3
|F1F2|=2c=8⇔c=4
c=
√a2−b2
c
2=a
2−b
2
16=a
2−9
a=5
========================
23 sty 16:01
 S=(5,1)
|PS|=b=3
|F1F2|=2c=8⇔c=4
c=√a2−b2
c2=a2−b2
16=a2−9
a=5
S=(5,1)
|PS|=b=3
|F1F2|=2c=8⇔c=4
c=√a2−b2
c2=a2−b2
16=a2−9
a=5