Wyznaczanie najmniejszej odległości od punktu. Pilecki: Witam, proszę o pomoc w zadaniu z geometrii analitycznej. Wyznacz na paraboli o równaniu y=¹₂ x² punkt, którego odległość od punktu A(8,−1) jest najmniejsza.Podaj tę odległość. Pozdrawiam.

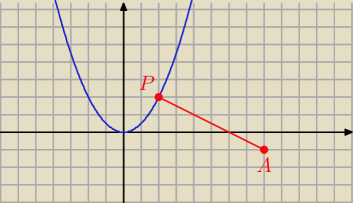
Janek191: P = (x , 0,5 x²) A = ( 8, − 1) Odległość d = √(8 − x)² + ( − 1 − 0,5 x²)² d − jest najmniejsza, gdy ( 8 − x)² + ( 1 + 0,5 x²)² jest najmniejsza f(x) = 64 − 16 x + x² + 1 + x² + 0,25 x⁴ = 0,25 x⁴ + 2 x² − 16 x + 65 więc f '(x) = x³ + 4 x − 16 = 0 ⇔ x = 2 f ''(x) = 3 x² + 4 f ''(2) > 0 − minimum dla x = 2 Wtedy f(2) = 0,5*2² = 2 P = ( 2, 2) ========= d = I A P I = √ 6² + 3² = √45 = 3√5