wartości funkcji (za 3 punkty) sam: Udowodnij, że funkcja f(x)=4x²+¹_x dla x>0, przyjmuje wartości niemniejsze od 3.

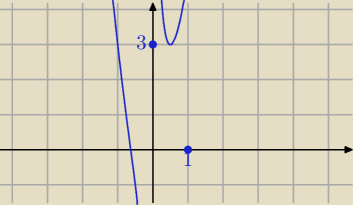
Janek191: Oblicz minimum lokalne

sam: Ok, funkcja w punkcie x=¹₂ ma minimum lokalne, i f(¹₂)=3. To wystarczy czy trzeba jakoś udowodnić słownie?

PW: Jeżeli nie ma przymusu stosowania rachunku różniczkowego, to wolę rozwiązanie elementarne (na pewno szybsze):

	1		1		1
4x2+		= 4x2+		+		≥33√4x2.12x.12x=33√1=3,
	x		2x		2x

nierówność jest zastosowaniem nierówności między średnią arytmetyczną a geometryczną dla trzech liczb dodatnich. Równość ma miejsce dla jednakowych składników, to znaczy dla x takiego że

	1
4x2=
	2x

	1
x=		.
	2