oblicz tgβ, sinβ, cosβ, ctgβ młodzik: W ostrosłupie prawidłowym czworokątnym α jest miarą kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstaw. β− miara kąta nachylenia sciany bocznej tego ostrosłupa do płaszczyzny podstawy. Wiadmomo ze tgα=1. oblicz tgβ, sinβ, cosβ, ctgβ. Wyjaśnij i udowodnij, skąd co wiesz.

młodzik: up

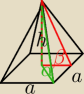
alinka: tgα=1= ^h_{1/2 a √2} tgβ= ^h_{1/2 a}

alinka: może ktoś inny pomoże dalej mi nic nieprzychodzi do głowy

alinka: a więc ^h_{1/2 a √2} = 1 to h=1/2 a √2 tgβ= {h}{1/2 a } = ^{1/2 a √2}_1/2a = ¹_√2

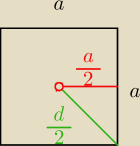
iteRacj@: rzut podstawy tego ostrosłupa skoro tgα=1

	h
to		=1
	d/2

	d
h=
	2

d=√2*a

	√2*a
h=
	2

	h
tgβ=
	a

.....