Optymalizacja Mikołaj: W okrąg o promieniu R wpisano prostokąt ABCD. Wyznacz możliwie największe pole tego prostokąta. robiłem to tak : wyznaczenie wzoru na pole P= xy z tw PG: x² + y² = (2r)² ==> x = √ 4r² − y² po podstawieniu P = √ (4r² − y²)y² Jaka będzie dziedzina? Jak ją wyznaczyć? Jak policzyć pochodną z tego ;x dodam, że jest to zadanie na poziomie licealnym

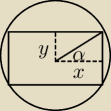
Jerzy: Prościej będzie uzależnić pole od kąta. P = 4*x*y = 2R²sin2α P' = 4R²cos2α ... i maksimum dla : α = 45⁰

Basia: możesz sobie ułatwić życie i sprawdzić kiedy P² jest największe, bo dla P>0 są to warunki równoważne dziedzina: 0 < x,y < 2r wynika wprost z treści zadania formalnie: (4r²−y²)*y²>0 ⇔ (2r−y)(2r+y)>0 (bo y² stale dodatnie) y∊(−2r;2r) i y>0 (jako długość boku) czyli y∊(0,2r)

Janek: Jerzy dzięki za pomysł ale niestety nie wiem jak takie coś robić, wszystkie zadania optymalizacyjne w szkole robiliśmy bez użycia kątów /funkcji trygonometryczne. Basia po wyznaczeniu tej dziedziny mam liczyć pochodna z y²(4r²−y²)? Czyli to będzie p'(x) =8r²y−4y³ Teraz to przyrownac do zera? Jak sobie poradzić z tym jeśli są dwie zamienne 😯

Basia: to nie są dwie zmienne; r jest parametrem f(y) = −y⁴+4r²y² f'(y) = −4y³+8r²y = −4y(y²−2r²) y>0 f'(y)=0 ⇔ y²−2r²=0 ⇔ y=r√2 y∊(0;r√2) ⇒ f'(y)>0 ⇒ f rośnie y∊(r√2;2r) ⇒ f'(y)<0 ⇒ f maleje y_max = r√2 x_max = √4r²−2r² = r√2

	r√2*r√2
Pmax =		= r2
	2

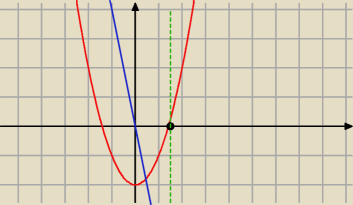
na rysunku masz wykres pochodnej czarna kropka to y=r√2