Rysowanie na płaszczyźnie zespolonej
kokos: Witam
Jak narysować na płaszczyźnie zespolonej
a)
A={z∊C : Im(2iz+3+2i)≤5}
b)
B={z∊C: |z+1+2i|<|z−3−2i|≤6}
c)
a)
2z+2≤5
nie wiem co dalej
b)
|z−(−1−2i)|<|z−(3+2i)|≤6
nie wiem jak narysować
c)
można po prostu podzielic przez 3?
wtedy będzie
proszę o wytłumaczenie do tych podpunktów
21 sty 22:21
kokos: pomógłby ktoś?
21 sty 22:40
kokos: 
22 sty 20:03
Mila:
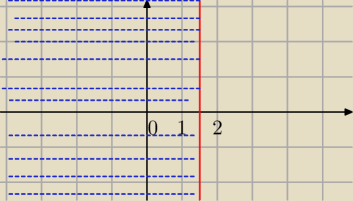
a) A={z∊C : Im(2iz+3+2i)≤5}
w=2i*z+3+2i
z=x+iy, xy∊R
w=2i*(x+iy)+3+2i=2x*i−2y+3+2i=(3−2y)+(2x+2)*i
Im(w)=2x+2
2x+2≤5
2x≤3
22 sty 20:27
kokos: dzięki, a w podpunkcie b jak narysować?
a w podpunkcie c można podzielić przez 3?
22 sty 20:41
Mila:
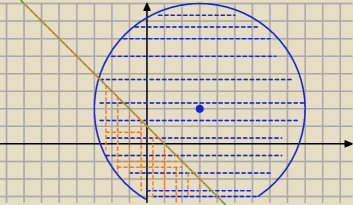
b) B={z∊C: |z+1+2i|<|z−3−2i|≤6}
|z−3−2i|≤6⇔|z−(3+2i|≤6 − koło o środku (3,2) i r=6
|z+1+2i|<|z−3−2i|
z=x+iy, x,y∊R
|x+iy+1+2i|<|x+iy−3−2i|
|(x+1)+(y+2)i|<|(x−3)+(y−2)|⇔
(x+1)
2+(y+2)
2<(x−3)
2+(y−2)
2⇔
x+y<1
y<−x+1
sprawdź np. dla z=(−1,1)
22 sty 20:42
Basia: Milu moim zdaniem wszystko się zgadza
robiłabym tak samo

22 sty 21:30
Mila:
Dziękuję bardzo
Basiu
22 sty 21:30

 a) A={z∊C : Im(2iz+3+2i)≤5}
w=2i*z+3+2i
z=x+iy, xy∊R
w=2i*(x+iy)+3+2i=2x*i−2y+3+2i=(3−2y)+(2x+2)*i
Im(w)=2x+2
2x+2≤5
2x≤3
a) A={z∊C : Im(2iz+3+2i)≤5}
w=2i*z+3+2i
z=x+iy, xy∊R
w=2i*(x+iy)+3+2i=2x*i−2y+3+2i=(3−2y)+(2x+2)*i
Im(w)=2x+2
2x+2≤5
2x≤3
 b) B={z∊C: |z+1+2i|<|z−3−2i|≤6}
|z−3−2i|≤6⇔|z−(3+2i|≤6 − koło o środku (3,2) i r=6
|z+1+2i|<|z−3−2i|
z=x+iy, x,y∊R
|x+iy+1+2i|<|x+iy−3−2i|
|(x+1)+(y+2)i|<|(x−3)+(y−2)|⇔
(x+1)2+(y+2)2<(x−3)2+(y−2)2⇔
x+y<1
y<−x+1
sprawdź np. dla z=(−1,1)
b) B={z∊C: |z+1+2i|<|z−3−2i|≤6}
|z−3−2i|≤6⇔|z−(3+2i|≤6 − koło o środku (3,2) i r=6
|z+1+2i|<|z−3−2i|
z=x+iy, x,y∊R
|x+iy+1+2i|<|x+iy−3−2i|
|(x+1)+(y+2)i|<|(x−3)+(y−2)|⇔
(x+1)2+(y+2)2<(x−3)2+(y−2)2⇔
x+y<1
y<−x+1
sprawdź np. dla z=(−1,1)

