Obrotowe krystian: 1.Stosunek pola powierzchni bocznej do pola powierzchni całkowitej stożka jest równy k. Wyznacz cosinus kąta rozwarcia stożka. 2.Stosunek objętości pola powierzchni całkowitej walca jest równy k. Przekrój osiowy tego walca jest prostokątem, w którym stosunek długości boków wynosi 2:3. Wyznacz promień podstawy i wysokość H tego walca.

	H		2
W 2 równanie kwadratowe z parametrem k i nie wiem co dalej , wychodzę od		=
	2r		3

	V		Hr
oraz		= k =>		= k
	Pc		2(r+1)

Eta:

	H		2		3H
2/		=		⇒ r=
	2r		3		4

V		πr2*H		rH
	=		=		= k
Pc		2πr(r+H		2r+2H

to

	2r+2H		1		2		2		1
		=		⇒		+		=		⇒
	rH		k		H		r		k

2		8		1		6+8		1
	+		=		⇒		=		⇒
H		3H		k		3H		k

	14k		14k
H=		to r=
	3		4

lub drugi przypadek:

	2r		2		H
		=		⇒ r=
	H		3		3

i dalej podobnie .....dokończ...........

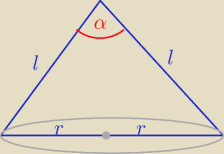Eta: 1/ z twierdzenia cosinusów

	l2+l2−(2r)2		2l2−4r2		r
cosα=		=		= 1−2(		)2
	2*l*l		2l2		l

2/ z treści zadania

πrl		l		r+l		1		r		1
	=k ⇒		=k ⇒		=		⇒		=		−1
πr(r+l)		r+l		l		k		l		k

r		1−k
	=
l		k

to cosα= .................. dokończ

krystian:

	8
drugi przypadek: r=		k H=8k
	3

1.

	−k2+4k−2		1
cosα =		, dla k <		, +∞)
	k2		2

krystian:

	1
W odpowiedziach k należy do przedziału <		, 1> Może mi ktoś wytłumaczyć czemu?
	2

krystian: Dobra, już chyba mam, chodzi o to, że Pb nie może być większe od Pc, dlatego k <1, k>0