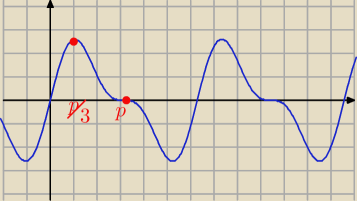
 p=π
p=π
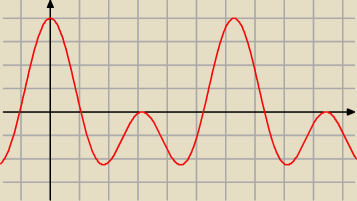 to jest wykres Twojej pochodnej; różni się od wykresu funkcji f'(t)=4t2+2t−2
to trzeba inaczej rozwiązać, ale na razie nie wiem jak
to jest wykres Twojej pochodnej; różni się od wykresu funkcji f'(t)=4t2+2t−2
to trzeba inaczej rozwiązać, ale na razie nie wiem jak
| 3π | ||
pochodna jest ciągła w przedziale <0; | > | |
| 2 |
| 3π | ||
f'( | ) = 4*0+2*0−2=−2 | |
| 2 |
| π | ||
czyli dla x∊<0; | ) f'(x)>0 ⇒ f rośnie | |
| 3 |
| π | ||
dla x∊( | ;π) f'(x)<0 ⇒ f maleje | |
| 3 |
| 3π | ||
dla x∊(π; | ) f'(x)<0 ⇒ f maleje | |
| 2 |
| π | ||
maksimum lokalne masz w p−cie x0= | ||
| 3 |
| √3 | 1 | 1+√3 | ||||
f(π/3) = 2* | + | = | ||||
| 2 | 2 | 2 |
| 1+√3 | ||
największą wartością jest f(π/3) = | ||
| 2 |
 cała rzecz polega na tym, że przy funkcjach trygonometrycznych miejsca zerowe wyznaczysz
sprowadzając pochodną do funkcji kwadratowej, ale wykres rzeczywistej pochodnej niewiele ma
wspólnego z wykresem funkcji kwadratowej
łatwo to sprawdzić porównując wykresy prostych funkcji y=cos2x i y=t2
trzeba wykombinować jak ta pochodna przebiega sprawdzając jej wartości na końcach przedziałów
tak jak to zrobiłam wyżej
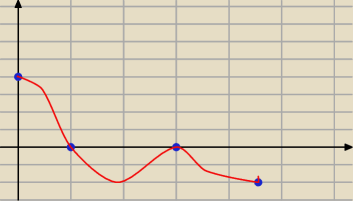
na tej podstawie prawdziwej pochodnej nie narysuję,ale przebieg tak
niebieskie kropki to te punkty (0;4) (π/3),0) (π,0) (3π/2, −2)
no to musi być mniej więcej taki przebieg jak tak czerwona krzywa
cała rzecz polega na tym, że przy funkcjach trygonometrycznych miejsca zerowe wyznaczysz
sprowadzając pochodną do funkcji kwadratowej, ale wykres rzeczywistej pochodnej niewiele ma
wspólnego z wykresem funkcji kwadratowej
łatwo to sprawdzić porównując wykresy prostych funkcji y=cos2x i y=t2
trzeba wykombinować jak ta pochodna przebiega sprawdzając jej wartości na końcach przedziałów
tak jak to zrobiłam wyżej
na tej podstawie prawdziwej pochodnej nie narysuję,ale przebieg tak
niebieskie kropki to te punkty (0;4) (π/3),0) (π,0) (3π/2, −2)
no to musi być mniej więcej taki przebieg jak tak czerwona krzywa