jaki jest wzór na pole czworokąta wklęsłewgo?
asia:
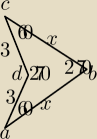
jaki jest wzór na pole czworokąta wklęsłewgo? w zadaniu mam podane dane ( na rysunku). i musze
obliczyc pole
20 sty 11:40
Jerzy:
Musisz podzielić na dwa trójkąty.
20 sty 11:41
Blee:
Chwila ... przy d i b masz taki sam kat 270 stopni
20 sty 11:43
młodzik: tak
20 sty 11:43
Blee: Tak jak Jerzy napisal.
Albo robisz linie DB i masz dwa trojkaty rozwartokatne (o znanych katach)
Albo robisz linie AC i masz dwa trojkaty rownoramienne (ABC I ACD) pole wiekszego minus pole
mniejsze to pole tegoz czworokata.
20 sty 11:45
asia: albo ja źle rozmiuem zadanie
20 sty 11:45
asia: treść: boki czworokąta wklęsłego są parami równej dł. mary dwóch kątów wew wynoszą 60 i 270.
oblicz pole pow. tego czworokąta, wiedząc ze krótszy bok ma dł 3
20 sty 11:47
Blee:
To jest bzdura z katami. Skoro katy przy d i b (zewnetrzny) sa takie same i rowne sa 270 stopni
to AB i AD sie przecinaja to wtedy CD i CB nie.moga sie przecinac.
Ponadto suma katow wewnetrznych w czworokacie wynos i 360 a tutaj wychodzi 480 stopni
20 sty 11:48
młodzik: własnie, czli nie umiem czytac poleceń, a jak w takim razie powiniem wyglądać rsunek
20 sty 11:49
Blee:
Dwa (z czterech) kataow maja miary 270 i 60
270 + 60 = 330
Czyli dwa pozostale katy maja w sumie 30 stopni.
Wiec przy b masz 60 przy a i c masz po 15.
Druga opcja (ze przy a i c masz 60) odpada bo bysmy mieli 270 + 2*60 + kat przy b = 390 + kat >
360
20 sty 11:50
asia: wydaje mi się czy to zadanie jest niepełne − młodzik czy ty tez tak zoribłeś, przygotowujesz
się do konkursu kuraotryjnego ?
20 sty 11:51
Blee:
Do obliczenia proponuje w takim razie zastosowac druga metode z tych co napisalem, czyli zrobic
linie AC i liczyc te pola trojkatow korzystajac z funkcji trygonometrycznych
20 sty 11:52
asia:
czy tak?
20 sty 11:53
Blee:
270 i 60 na odwrot ... pomysl ... 60 to kat OSTRY, a 270 to kat ROZWARTY ty zaznaczyles/−as
odwrotnie.
20 sty 11:54
Satan: @
asia, piszesz do
młodzika, tylko... Po co pisać sam ze sobą?
Podpowiem: dzieląc tę figurę dostajesz dwa trójkąty przystające z cechy bbb, więc pole figury =
2P
Δ
20 sty 12:02
młodzik: czy pole to 9(√3−1)2 ?
22 sty 16:52
22 sty 16:53
młodzik: dzięki a pole? dobre?
22 sty 17:01
kochanus_niepospolitus:
| | 3+x | | 3 | | 3(√3+1) | |
√3 = tg60o = |
| ⇔ x√3 − x = 3 ⇔ x = |
| = |
| |
| | x | | √3−1 | | 2 | |
I mamy:
P = (3+x)
2 − 3
2 − 3*x = 3x + x
2 ... podstawiasz i masz
22 sty 17:07