| (x+1)2 | ||
Mianowicie mam funkcje f(x)= | ||
| 2x |
| x2−1 | |
| 2x2 |
| (2x)(2x2)−(x2−1)(4x) | 1 | |||
A więc druga pochodna wychodzi: | = | |||
| 4x4 | x3 |
 Proszę o podpowiedź co robię źle
Proszę o podpowiedź co robię źle 
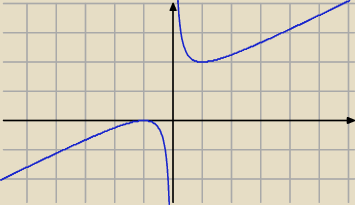 f ''(x) > 0 ⇔ x3 > 0 ⇔ x > 0 − f jest wypukła
f ''(x) < 0 ⇔ x3 < 0 ⇔ x < 0 − f jest wklęsła
f ''(x) > 0 ⇔ x3 > 0 ⇔ x > 0 − f jest wypukła
f ''(x) < 0 ⇔ x3 < 0 ⇔ x < 0 − f jest wklęsła
 Myślałem, że mam coś źle
Myślałem, że mam coś źle
| x2−1 | 1 | 1 | ||||
f'(x)= | = | − | x−2, a więc f''(x) obliczamy "jednym pociągnięciem". | |||
| 2x2 | 2 | 2 |