rozwiąż graficznie uklad nierowności: |x| ≤3 x + 2y < 3 młodzik: rozwiąż graficznie uklad nierowności: |x| ≤3 x + 2y < 3

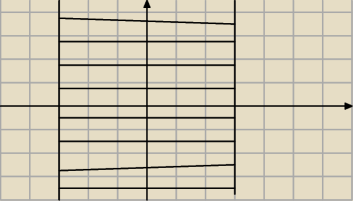
6-latek: a) razem z prostymi x=3 i x=−3

PW: To na razie pierwsza nierówność (potraktowana jako nierówność 2 zmiennych x i y). Trzeba na tym samym wykresie dorysować rozwiązania drugiej i wziąć część wspólną.

6-latek: Nie doczytalem . To ma byc uklad .

młodzik: pomoże ktoś? kiedy w nieówności jest i a kiedy lub (jak by można na przykładzie |x| ≤3 pokazać

PW: Ponieważ jest to układ nierówności dwóch zmiennych (widać to po drugiej nierówności), pierwszą należy traktować jako |x|≤3 i y dowolna. Taka jest niepisana umowa − jeżeli o zmiennej nie mówi się nic, to znaczy że jest dowolna. Dlatego 6−latek narysował rozwiązanie pierwszej nierówności jako zbiór par (x,y), takich że −3≤x≤3 ∧ y∊R. To jest dobrze narysowane. Ponieważ ilustrować mieliśmy rozwiązanie układu nierówności, trzeba jeszcze na tym samym rysunku zaznaczyć zbiór tych par (x,y|), dla których

	1		3
y<−		x+		,
	2		2

czyli punkty płaszczyzny leżące poniżej prostej

	1		3
y=−		x+
	2		2

i wziąć część wspólną obu rozwiązań.

Satan: @młodzik, spójnik "i" masz dla znaku mniejszości, spójnik "lub" dla znaku większości, jeśli chodzi o wartość bezwzględną. Przykładowo: |x| ≤ 3 ⇒ −3 ≤ x ≤ 3, czyli: x ≤ 3 ⋀ x ≥ −3 Warto sobie popatrzeć na przykładach jak wyglądają nierówności z wartością bezwzględną na osi liczbowej

młodzik: dziękuję, srednio rozumiem, ale dzięki i tak.

młodzik: @Satan dziękuję