równoliczność zbioru z R Natalia: Dowieść, że zbiór ma moc continuum (tzn R) {<x,y> ∊ R² : x≤0 ∧ y≤0 ∧2y+x ≥ −2}

Natalia: Up

Natalia: Up, bardzo proszę.

g: Zaczął bym od kwadratu o rogach (0,0), (0,1), (1,1), (1,0) i pokazał że moc zbioru punktów jest R Każdej parze liczb (x,y) takich, że 0 ≤ x,y ≤ 1 da się jednoznacznie przyporządkować liczbę z ∊ [0,1]. np. x = 0.1357..., y = 0.2468..., to z = 0.12345678.... Jeśli teraz mamy jakiś obszar zamknięty to można znaleźć kwadrat, który w całości go zawiera, oraz drugi kwadrat, który w całości się zawiera w obszarze. Moce zbiorów punktów obu tych kwadratów są R, więc moc obszaru też jest R.

Natalia:

	1		1
A gdyby zrobić sobie kwadracik jako zbiór B= {<x,y> : x∊[−		,0] ∧y∊[−		,0]}
	2		2

	1
Bo dla dolnych wartości x i y mamy że −1−		≥ −2
	2

Wiemy że B jest równoliczny z R² tzn z c (Continuum). No I tez B⊆ A ⊆ R² Istnieje jakaś bijekcja F:R→B np. F(x)=<x,0> Co dowodzi że |B| = c

Natalia: I wtedy skoro |B| = c to Skoro A zawiera B. To A również jest continuum

Natalia: Może być takie coś?

Natalia: Tzn tam miało być nie dla dowolnych tylko dla najmniejszych wartości x i y

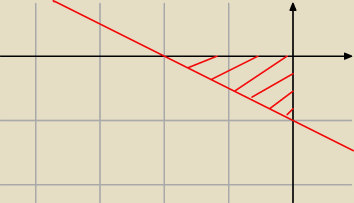
g: A nie wystarczy pokazać że obszar z zadania jest ciągły i ograniczony? Zresztą nieograniczoność nie przeszkadza. Nieciągłość mogła by coś zmienić, mogło by się okazać że punktów jest przeliczalnie wiele.

Adamm: ciągłość to chyba nie jest słowo którego szukałeś

Adamm: to proste zadanie bierzesz odcinek, jest mocy continuum, jest podzbiorem tego zbioru ten zbiór jest podzbiorem całej płaszczyzny, ona jest mocy continuum więc sam zbiór jest mocy continuum