geometria analityczna asd: Punkty A(0,−5) oraz D(−3,−1) są kolejnymi wierzchołkami trapezu równoramiennego ABCD, którego osią symetrii jest prosta o równaniu x+2y=0. Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramion tego trapezu. Mógłby ktoś mnie naprowadzić na rozwiązanie?

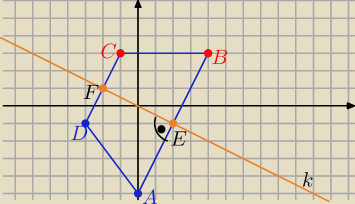
Eta: k⊥AB i k⊥DC

	1
k: y= −		x
	2

to AB: y= 2(x−x_A)+y_A ⇒ y=2x−5 k∩AB={E} ⇒ 2x−5= −0,5x ⇒ ... x= 2 to y= −1 E(2,−1) E jest środkiem AB więc x_B= 2x_E−x_A i y_B=2y_E−y_A ⇒ ........... B(4,3) podobnie: prosta DC: y= 2(x−x_D)+y_D ⇒ y= 2x+5 k∩DC={F} ⇒ 2x+5= −0,5x ⇒ ............. F jest środkiem DC ........... .................. dokończ

asd: dziękuję!

Eta: