pole obszaru między krzywymi maksiu: Oblicz pole obszaru ograniczonego liniami: y² = 2x + 1, x − y − 1 = 0 ⇒y = x − 1 Punkty wspólne to: 2x + 1 = (x − 1)² x² − 4x = 0 x = 0 ⋁ x = 4 |P| = ∫[√2x + 1 − (x − 1)]dx (od 0 do 4)

	1		1
|P| =		(2x + 1)32 −		x2 + x w granicach 0, do 4
	3		2

	1		1		14
|P| = (		*27 − 8 + 4) − (		− 0 + 0) =
	3		3		3

	16
a w odpowiedziach jest
	3

Zamiast odjąć mam dodać? Coś źle zrozumiałem? Próbowałem robić, że odejmowałem w całce od x − 1 ten pierwiastek i wtedy po wyliczeniu wychodziło −{16}{3} ale pole nie może być ujemne Potrzebuję, żeby ktoś sprawdził i powiedział jaki jest błąd

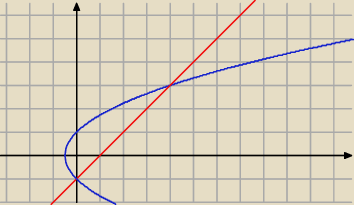
Basia: popatrz na wykres; brakuje Ci tego fragmentu na lewo od osi OY równanie y² = 2x+1 opisuje tę niebieską krzywą to się przekłada na dwa równania y=√2x+1 lub y=−√2x+1

	1
gdzie 2x+1≥0 czyli x≥−
	2

	1
P = to co sam napisałeś + ∫(√2x+1−(−√2x+1) dx w granicach od −		;0
	2

albo po prostu

	1
P = to co sam napisałeś + 2∫(√2x+1 dx w granicach −		;0
	2

maksiu: Ach dziękuję, teraz rozumiem, widzę że popełniałem błąd o którym nie wiedziałem też przy robieniu innych przykładów