zadanie
jaro: W trójkącie równoramiennym ABC takim, że |AC|=|BC|, poprowadzono wysokość AD.
Wysokość ta podzieliła ramię BC na odcinki |BD|=a i |CD|=3a.
Wykaż, że podstawa trójkąta ma długość 2√2a.
18 sty 21:16
Eta:
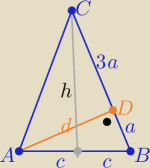
P
2(ABC)=h
2*c
2 i P
2(ABC)= d
2*4a
2
i h
2=16a
2−c
2 i d
2= 4c
2−a
2
16a
2c
2−c
4= 16a
2c
2−4a
4 ⇒ c
2=2a
2 ⇒ c=
√2a
to 2c=|AB|=2
√2a
===============
18 sty 21:30
Janek191:
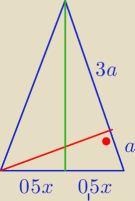
Z podobieństwa Δ mamy
x
2 = 8 a
2
x = 2
√2 a
==============
18 sty 21:34
Eta:
2 sposób
Z podobieństwa trójkątów ADB i EBC z cechy (kkk) E −− spodek wysokości h
| 2c | | a | |
| = |
| ⇒2c2=4a2 ⇒ c=√2a |
| 4a | | c | |
to |AB|=2c=2
√2a
18 sty 21:34
Mila:
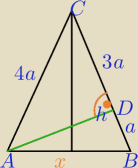
Dwa razy tw.Pitagorasa.
W ΔADC i ΔADB
18 sty 21:35
Eta:
No i sypnęło kilkoma sposobami
18 sty 21:36
Eta:
To jeszcze sposobem
Mili
h
2=16a
2−9a
2= 7a
2 i h
2= x
2−a
2
x
2−a
2=7a
2 ⇒ x
2=8a
2 ⇒ x=|AB|=2
√2a
18 sty 21:40