prawdopodobienstwo tysia: W pierwszej urnie są kule czarne i białe. W drugiej urnie jest 6 kul niebieskich i 4 zielone, a w trzeciej urnie są 2 kule niebieskie i 8 zielonych. Losujemy jedną kulę z pierwszej urny. Jeśli wylosowana kula jest czarna to losujemy jedną kulę z drugiej urny, a jeśli biała to losujemy jedną kulę z trzeciej urny. Prawdopodobieństwo wylosowania kuli zielonej jest dwa razy większe od prawdopodobieństwa wylosowania kuli niebieskiej. Obliczyć prawdopodobieństwo wylosowania kuli czarnej. mam do wyboru 3/4, 1/3, 2/3, 1,4

iteRacj@:

4
	− prawdopodobieństwo wylosowania kuli zielonej z II urny
10

6
	− prawdopodobieństwo wylosowania kuli niebieskiej z II urny
10

8
	− prawdopodobieństwo wylosowania kuli zielonej z III urny
10

2
	− prawdopodobieństwo wylosowania kuli niebieskiej z III urny
10

b − ilość kul białych w I urnie c − ilość kul czarnych w I urnie

b
	− prawdopodobieństwo wylosowania kuli białej z I urny
b+c

c
	− prawdopodobieństwo wylosowania kuli czarnej z I urny
b+c

c		4		b		8
	*		+		*		− prawdopodobieństwo wylosowania kuli zielonej
b+c		10		b+c		10

c		6		b		2
	*		+		*		− prawdopodobieństwo wylosowania kuli niebieskiej
b+c		10		b+c		10

prawdopodobieństwo wylosowania kuli zielonej jest dwa razy większe od prawdopodobieństwa wylosowania kuli niebieskiej

c

4

b

8

c

6

b

2

*

+

*

= 2*[

*

+

*

]

b+c

10

b+c

10

b+c

10

b+c

10

4c+8b=12c+4b b=2c ilość kul białych jest dwa razy większa od ilości kul czarnych wniosek ...

Eta: Odp: P(cz)=1/3

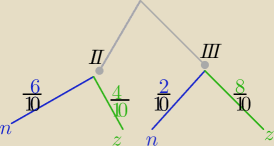
Eta: @iteR@cja Nie przepadam za "krzakami" ale w tym wypadku szanujemy czas na maturze! i dalej już.................

	a		b
P(Z)=2P(N) i P(C)=		i P(B)=
	a+b		a+b

....................... Miłego wieczoru

Pytający: Można też tak: x∊<0,1> // prawdopodobieństwo wylosowania kuli czarnej 1−x // prawdopodobieństwo wylosowania kuli białej P(zielona)=2P(niebieska) 4x+8(1−x)=2(6x+2(1−x)) 12x=4

	1
x=
	3

I również miłego wieczoru!

tysia: dziękuję Wam!

iteRacj@: i ja bardzo dziekuję za wskazówki! rozwiązywanie zadań to nie góry, trzeba chodzić najprostszymi drogami...