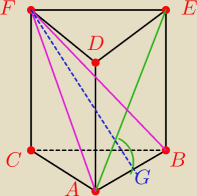
 Dany jest graniastosłup prosty prawidłowy trójkątny o dolnej podstawie ABC i górnej A'B'C'.
Przekątna ściany bocznej tworzy z krawędzią podstawy kąt 60°. Pole ściany bocznej
graniastosłupa jest równe 2√3. Oblicz pole trójkąta ABC'.
Uwaga: w programie do rysowania nie da się wpisać dwóch znaków (albo nie potrafię), więc
zmieniam oznaczenia: A' = D, B' = E, C' = F
Więc zrobiłem to tak: Skoro jest to graniastosłup prosty prawidłowy trójkątny, to |AB| = |BC| =
|AC| = a. |∡BAE| = 60° i |∡ABE| = 90°, bo ściany są prostokątami.
Dany jest graniastosłup prosty prawidłowy trójkątny o dolnej podstawie ABC i górnej A'B'C'.
Przekątna ściany bocznej tworzy z krawędzią podstawy kąt 60°. Pole ściany bocznej
graniastosłupa jest równe 2√3. Oblicz pole trójkąta ABC'.
Uwaga: w programie do rysowania nie da się wpisać dwóch znaków (albo nie potrafię), więc
zmieniam oznaczenia: A' = D, B' = E, C' = F
Więc zrobiłem to tak: Skoro jest to graniastosłup prosty prawidłowy trójkątny, to |AB| = |BC| =
|AC| = a. |∡BAE| = 60° i |∡ABE| = 90°, bo ściany są prostokątami.
| |EB | h | |||
Więc tg 60° = | i niech |EB| = h ⇒ √3 = | ⇒ h = a√3. | ||
| |AB| | a |
| √2 | ||
więc |GB| = | . Z tw. Pitagorasa w ΔGBF: | |
| 2 |
| 2 | 30 | √30 | ||||
|FG| = √|FB|2 − |GB|2 ⇒ |FG| = √8 − | ⇒ |FG| = √ | ⇒ |FG| = | . | |||
| 4 | 4 | 2 |
| 1 | 1 | √30 | 2√15 | √15 | ||||||
PΔABF = | * |AB| * |FG| = | * √2 * | = | = | ||||||
| 2 | 2 | 2 | 4 | 2 |
| √15 | ||
Czyli PΔABF = | ||
| 2 |

 Masz dobrze
Masz dobrze  ale ogrom czasu marnujesz ...............
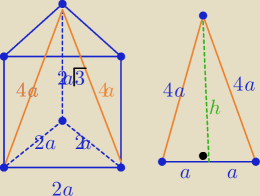
Trójkąt "ekierka" i odpowiednie oznaczenia ułatwiają rozwiązanie
ale ogrom czasu marnujesz ...............
Trójkąt "ekierka" i odpowiednie oznaczenia ułatwiają rozwiązanie
| 1 | ||
P(ściany)= 4a2√3=2√3 ⇒ a2= | ||
| 2 |
| √15 | ||
PΔABF = a*h= a2√15= | [j2] | |
| 2 |
 Jeszcze nad tym popracuję, dziękuję Eta
Jeszcze nad tym popracuję, dziękuję Eta 
