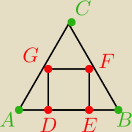
Planimetria Satan: Wyznacz długość boku kwadratu wpisanego w trójkąt równoboczny o boku a w ten sposób, że jeden bok kwadratu jest zawarty w boku trójkąta, a dwa wierzchołki kwadratu należą do pozostałych boków trójkąta, Znów się upewniam Zaczynam od tego, że skoro ΔABC jest równoboczny, to |AB| = |BC| = AC| i |∡ACB| = |∡ABC| = |∡BAC| = 60°. Teraz oznaczam sobie, że kwadrat DEFG ma bok długości x. ΔGFC ~ ΔABC z cechy kkk, więc jest równoboczny o boku x. W takim razie odcinek |AG| = a − x, bo jest równy |AC| − |GC|. ΔADG jest prostokątny, bo |∡EDG|

	|DG|		x		√3
= 90°, więc |∡ADG| = 90°. W takim razie: sin 60° =		⇒		=		⇒
	|AG|		a−x		2

x = a(2√3 − 3} Czyli x = a(2√3 − 3)

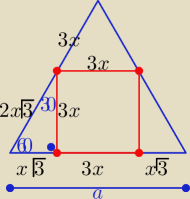Eta: Można też tak : wykorzystać własność trójkąta "ekierki" dł. boku kwadratu oznaczam 3x to a= 3x+2x√3 ⇒ x(2√3+3)=a /*(2√3−3) ⇒ 3x=(2√3−3)a ===========

Satan: Sprytnie, na to bym nie wpadł Jeszcze trochę muszę poćwiczyć, dziękuję Eta