proszę o rozwiązanie Anna: X jest zbiorem całkowitych wartości parametru m dla których równanie I − x² + 2 IxI +5 I = m ma cztery rozwiązania oblicz sumę sześcianów liczb należących do zbioru X zakoduj cyfry setek dziesiątek i jedności otrzymanego wyniku x₁³ + x₂³ = ( x₁ + x₂)( x₁² − x₁x₂ +x₂) wynik to 316 ale rozwiązując według wzoru nie mam takiego wyniku

Jerzy: A co to są x₁ oraqz x₂ ?

PW: Anno, przede wszystkim masz obliczyć sumę sześcianów tych m, dla których równanie ma 4 rozwiązania − to nie ma nic wspólnego z rozwiązaniami x₁, x₂, x₃, x₄.

Anna: czyli − x2 + 2 IxI +5 = m dla x ≥0 lub dla x < 0 − x2 + 2 x +5 = m lub − x2 − 2x +5 = m − x2 + 2 x +5 − m = 0 − x2 − 2x +5 − m =0 dalej Δ

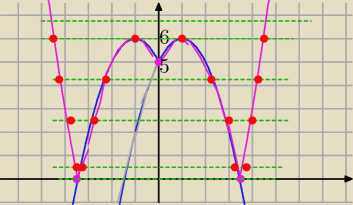
Eta: Proponuję tak graficznie Narysuj wykres 1/ y= −x²+2x+5 2/ y= −x²+2|x|+5 3/ y= |−x²+2|x|+5| i tnij prostą y=m cztery rozwiązania będą dla m∊(0,5) U{6} zatem całkowite m to: 1,2,3,4,6 1³+2³+3³+4³+6³ = 316

Janek191: − x² = − I x I²

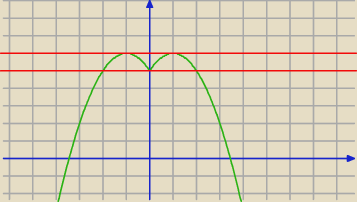
PW: Dobrze by było sporządzić wykresy (ten jest dla −x²+2|x|+5 i czerwone linie y=6 i y=5 pokazują, że nie ma całkowitej m, dla której badane równanie miałoby 4 rozwiązania). Na pewno dobrze przepisana treść zadania?

Eta:

PW: Eta jak zwykle niezawodna. miałem ten sam pomysł z graficznym rozwiązaniem, tylko realizacja do dupy, czy jak to tam elegancko mówią.

Anna: zadanie dobrze przepisane z " Teraz matura 2016 " poziom rozszerzony − zad 7 str20 wydanie Nowa Era z 2015 r dziękuję bardzo