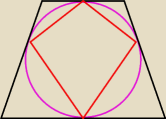
Trapez Iza: Trapez równoramienny opisany jest na okręgu o promieniu 1. Pole trapezu wynosi 5. a) znajdz długość ramienia trapezu. b)oblicz pole czworokąta, którego wierzchołkami sa punkty styczności okręgu z trapezem.

Bogdan:

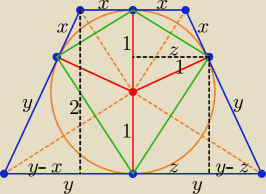
	x		1
Z podobieństwa trójkątów:		=		⇒ xy = 1
	1		y

	1		1		1		5
Pole trapezu:		*2y*1 +		*2x*1 + 2*		(x + y)*1 = 5 ⇒ x + y =
	2		2		2		2

	5
Po rozwiązaniu układu równań: xy = 1 i x + y =		przy założeniach: x > 0, y > 0,
	2

	1
y > x, otrzymujemy: x =		i y = 2
	2

	y − x		y − z		1,5		2 − z
Z podobieństwa trójkątów:		=		⇒		=		⇒
	y + x		y		2,5		2

	4
⇒ z =
	5

	1		4		8
Pole czworokąta (zielonego) P = 2*		*2r*z = 2*		=
	2		5		5

asdsadasd: ⇔