wykaz,ze
Daniel:
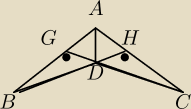
Korzystając z podanych niżej informacji,wykaz,że odcinek AD zawiera się w dwusiecznej kąta BAC.
(rysunek troszke zbyt krotki)
Mozna opisac na tym okrąg i:
∡BAC=α
∡BDC=2α zatem wysokosc jest dwusieczną c.k.d
Można tak zrobić ?

Satan:
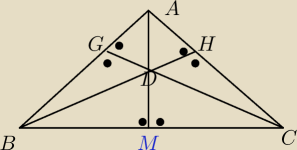
Więc, mam nadzieję, że nie myślę błędnie. Figura jest wpisana w okrąg wtedy i tylko wtedy, gdy
wszystkie wierzchołki figury leżą na okręgu. A tutaj jak widać jest to niemożliwe, bo mamy do
czynienia z wielokątem niewypukłym.
Zrobiłbym to tak:
|∡BDG| = |∡CDH|, bo proste BH i CG przecinają się w jednym punkcie i tworzą kąty wierzchołkowe.
W takim wypadku również |∡DBG| = |∡DCH|.
ΔAGD i ΔADH są prostokątne. Kąty |∡BDM| i |∡HDM| są równe (wierzchołkowe) i |∡CDM| = |∡GDA| są
również równe.
Teraz: |∡BDM| + |∡BDG| + |∡ADG| = 180° = |∡CDM| + |∡CDH| + |∡HDA|. Zamieniając kąty mamy:
|∡BDM| + |∡BDG| + |∡ADG| = |∡ADG| + |∡BDG| + |∡BDM|. L = P, więc |∡ADG| = |∡HDA|.
Skoro ΔADG i ΔADH są prostokątne i mają dwa identyczne kąty, to znaczy, że trzeci kąt również
jest równy trzeciemu kątowi drugiemu trójkąta. W takim razie Odcinek |AD| jest dwusieczną.
Pewnie da się to zrobić szybciej

 Korzystając z podanych niżej informacji,wykaz,że odcinek AD zawiera się w dwusiecznej kąta BAC.
(rysunek troszke zbyt krotki)
Mozna opisac na tym okrąg i:
∡BAC=α
∡BDC=2α zatem wysokosc jest dwusieczną c.k.d
Można tak zrobić ?
Korzystając z podanych niżej informacji,wykaz,że odcinek AD zawiera się w dwusiecznej kąta BAC.
(rysunek troszke zbyt krotki)
Mozna opisac na tym okrąg i:
∡BAC=α
∡BDC=2α zatem wysokosc jest dwusieczną c.k.d
Można tak zrobić ?
 Więc, mam nadzieję, że nie myślę błędnie. Figura jest wpisana w okrąg wtedy i tylko wtedy, gdy
wszystkie wierzchołki figury leżą na okręgu. A tutaj jak widać jest to niemożliwe, bo mamy do
czynienia z wielokątem niewypukłym.
Zrobiłbym to tak:
|∡BDG| = |∡CDH|, bo proste BH i CG przecinają się w jednym punkcie i tworzą kąty wierzchołkowe.
W takim wypadku również |∡DBG| = |∡DCH|.
ΔAGD i ΔADH są prostokątne. Kąty |∡BDM| i |∡HDM| są równe (wierzchołkowe) i |∡CDM| = |∡GDA| są
również równe.
Teraz: |∡BDM| + |∡BDG| + |∡ADG| = 180° = |∡CDM| + |∡CDH| + |∡HDA|. Zamieniając kąty mamy:
|∡BDM| + |∡BDG| + |∡ADG| = |∡ADG| + |∡BDG| + |∡BDM|. L = P, więc |∡ADG| = |∡HDA|.
Skoro ΔADG i ΔADH są prostokątne i mają dwa identyczne kąty, to znaczy, że trzeci kąt również
jest równy trzeciemu kątowi drugiemu trójkąta. W takim razie Odcinek |AD| jest dwusieczną.
Pewnie da się to zrobić szybciej
Więc, mam nadzieję, że nie myślę błędnie. Figura jest wpisana w okrąg wtedy i tylko wtedy, gdy
wszystkie wierzchołki figury leżą na okręgu. A tutaj jak widać jest to niemożliwe, bo mamy do
czynienia z wielokątem niewypukłym.
Zrobiłbym to tak:
|∡BDG| = |∡CDH|, bo proste BH i CG przecinają się w jednym punkcie i tworzą kąty wierzchołkowe.
W takim wypadku również |∡DBG| = |∡DCH|.
ΔAGD i ΔADH są prostokątne. Kąty |∡BDM| i |∡HDM| są równe (wierzchołkowe) i |∡CDM| = |∡GDA| są
również równe.
Teraz: |∡BDM| + |∡BDG| + |∡ADG| = 180° = |∡CDM| + |∡CDH| + |∡HDA|. Zamieniając kąty mamy:
|∡BDM| + |∡BDG| + |∡ADG| = |∡ADG| + |∡BDG| + |∡BDM|. L = P, więc |∡ADG| = |∡HDA|.
Skoro ΔADG i ΔADH są prostokątne i mają dwa identyczne kąty, to znaczy, że trzeci kąt również
jest równy trzeciemu kątowi drugiemu trójkąta. W takim razie Odcinek |AD| jest dwusieczną.
Pewnie da się to zrobić szybciej 