Oblicz pole powierzchni całkowitej ostrosłupa Aheryt: Podstawą ostrosłupa ABCS jest trójkąt prostokątny o kącie prostym w wierzchołku C. Promień okręgu opisanego na tym trójkącie jest równy 3. Ściany boczne ACS i BCS są prostopadle do podstawy. Pole ściany ABS jest równe 12√2 i jest ona nachylona do podstawy pod kątem 60 stopni. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Pole podstawy wyszło mi 6√2, wysokość ostrosłupa to odcinek CS, który wynosi 2√6, więc objętość to 8√3. Mam jednak problem z obliczeniem pola całkowitego (a dokładniej pola bocznego). Z góry dziękuję za pomoc!

Aheryt: Wynik to P = 12(1+2√2)

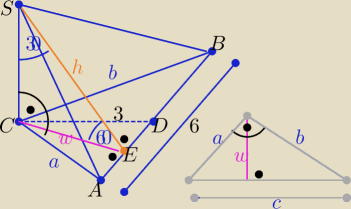
Eta: V=8√3 −−− masz dobrze H= 2√6 i P_p=6√2 też i |AB|=2R=6=c P(ABS)=12√2 ⇒ 3*6=12√2 ⇒ |SE|=h=4√2 w trójkącie SCE "ekierce" w= 2√2

	ab
w Δprostokątnym w=		⇒ ab=c*w ⇒ ab= 12√2
	c

P_c= P_p+P(ABS)+ P(ACS)+P(BCS)

	1
Pc= 18√2+		H(a+b)= 18√2+√6(a+b)
	2

w Δ ABC : a²+b²=6² ⇒ (a+b)²−2ab=36⇒ (a+b)²=24√2+36= 4(6√2+9) to (a+b) = 2√6√2+9 P_c= 18√2+2√6*√6√2+9= 18√2+2√2*√3*√6√2+9= = 18√2 +2√2*√18√2+27 oraz 18√2+27= (3√2+3)² P_c= 18√2+2√2*(3√2+3)=........................= 12(1+2√2)