 2. Punkty A(0.0) I B(10,0) są wierzhołkami trójkąta prostokątnego o kącie prostym przy
wierzchołku C.
Przyprostokątna AC jest zawarta w prostej y=3x. Wyznacz współrzędne punktu C oraz współrzędne
środka okręgu opisanego na tym trójkącie.
tutaj jestem całkowicie zielona.
3. Dane są punktyA(0,0) B(10,10) i C(4,13). Z wierzchołka A trójkąta ABC poprowadzono wysokość
AD.
Wyznacz współrzędne punktu D i oblicz pole trójkąta ABC.
Obiczyłam AB,które wyszło mi 2√10.Środek obliczyłam i otrzymałam wynik (7,13),a w
odpowiedziach
jest wynik (6,12).
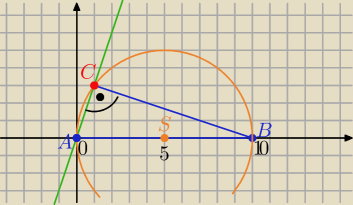
2. Punkty A(0.0) I B(10,0) są wierzhołkami trójkąta prostokątnego o kącie prostym przy
wierzchołku C.
Przyprostokątna AC jest zawarta w prostej y=3x. Wyznacz współrzędne punktu C oraz współrzędne
środka okręgu opisanego na tym trójkącie.
tutaj jestem całkowicie zielona.
3. Dane są punktyA(0,0) B(10,10) i C(4,13). Z wierzchołka A trójkąta ABC poprowadzono wysokość
AD.
Wyznacz współrzędne punktu D i oblicz pole trójkąta ABC.
Obiczyłam AB,które wyszło mi 2√10.Środek obliczyłam i otrzymałam wynik (7,13),a w
odpowiedziach
jest wynik (6,12).
 2/
AC : y=3x to aAC=3
2/
AC : y=3x to aAC=3
| 1 | ||
BC⊥AC więc aBC= − | ||
| 3 |
| 1 | 10 | |||
prosta BC : y= −1/3(x−xB) ⇒ BC: y= − | x+ | |||
| 3 | 3 |
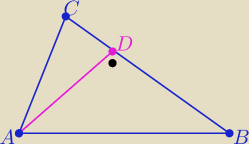 3/
Podaję jeden ze sposobów
Proste AD ⊥BC współczynniki kierunkowe
3/
Podaję jeden ze sposobów
Proste AD ⊥BC współczynniki kierunkowe
| 13−10 | 1 | |||
aBC= | = − | to aAD= 2 | ||
| 4−10 | 2 |
| 1 | ||
BC : y= − | (x−10)+10 i AD : y=2x | |
| 2 |
| 1 | ||
P(ABC)= | |AB|*h=.......... | |
| 2 |
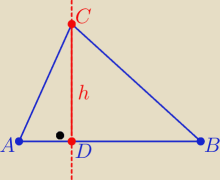 1/
Masz dobrze
teraz tak
Prosta CD ma równanie y=2x+2 to C(x, 2x+2)
Odległość punktu C od prostej AB to h= 2√5
Napisz równanie prostej AB ⊥ CD w postaci ogólnej
1/
Masz dobrze
teraz tak
Prosta CD ma równanie y=2x+2 to C(x, 2x+2)
Odległość punktu C od prostej AB to h= 2√5
Napisz równanie prostej AB ⊥ CD w postaci ogólnej
| 1 | ||
AB: y= − | (x−xA)+yA | |
| 2 |
| |x+2(2x+2)+2| | |
=2√5 | |
| √5 |
 !
! 